-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 5.1, 5.2, 5.3, 5.4 phần bài tập bổ sung trang 146, 147 SBT toán 7 tập 1
Giải bài 5.1, 5.2, 5.3, 5.4 phần bài tập bổ sung trang 146, 147 sách bài tập toán 7 tập 1. Cho tam giác ABC và tam giác có ba đỉnh là D, E, F, ...
Bài 5.1
Cho tam giác \(ABC\) và tam giác có ba đỉnh là \(D,E,F\). Biết \(AB= DF\) và \(\widehat B = \widehat D\)
Trong các khẳng định sau,khẳng định nào đúng, khẳng định nào sai ?
a) Nếu \(\widehat A = \widehat F\) thì hai tam giác đó bằng nhau.
b) Nếu \(\widehat A = \widehat E\) thì hai tam giác đó bằng nhau.
c) Nếu \(\widehat C = \widehat E\) thì hai tam giác đó bằng nhau.
Phương pháp giải:
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Lời giải chi tiết:
Nếu hai tam giác trên bằng nhau, ta có:
Vì \(\widehat B = \widehat D\) suy ra đỉnh \(B\) tương ứng với đỉnh \(D\).
Vì \(AB= DF\) suy ra đỉnh \(A\) tương ứng với đỉnh \(F\).
Do đó đỉnh \(C\) tương ứng với đỉnh \(E\).
a) Đúng;
b) Sai;
c) Đúng.
Bài 5.2
Cho tam giác \(ABC\) trên tia đối của tia \(AB\) lấy điểm \(D\) sao cho \(AD=AB\). Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE=AC.\) Một đường thẳng đi qua \(A\) cắt \(DE\) và \(BC\) theo thứ tự tại \(M\) và \(N.\) Chứng minh rằng:
a) \(BC // DE\).
b) \(AM = AN\).
Phương pháp giải:
- Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết:
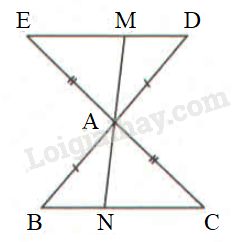
a) Xét \(ΔABC\) và \(ΔADE\) có:
\(AB = AD\) (gt)
\(AC = AE\) (gt)
\(\widehat {BAC} = \widehat {DAE}\) (hai góc đối đỉnh)
\(⇒ ΔABC = ΔADE\) (c.g.c)
\(⇒ \widehat C = \widehat E\) (hai góc tương ứng)
Mà \(\widehat C \) và \( \widehat E\) ở vị trí so le trong nên \(DE // BC.\)
b) Xét \(ΔAEM\) và \(ΔACN\) có:
\( \widehat E= \widehat C \) (chứng minh trên)
\(AE = AC\) (gt)
\(\widehat {EAM} = \widehat {CAN}\) (hai góc đối đỉnh)
\(⇒ ΔAEM = ΔACN\) (g.c.g)
\(⇒ AM = AN\) (hai cạnh tương ứng).
Bài 5.3
Chứng minh rằng nếu hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau.
Phương pháp giải:
Nếu cạnh huyền và góc nhọn của tam giác vuông nay bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Lời giải chi tiết:
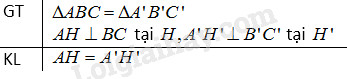
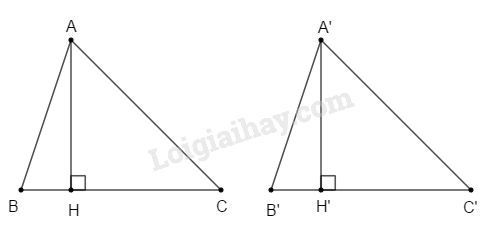
Xét \( ΔABC = ΔA'B'C'\). Kẻ \(AH ⊥ BC, A’H’ ⊥ B’C’\).
Vì \( ΔABC = ΔA'B'C'\)
\( \Rightarrow AC = A’C’\) (hai cạnh tương ứng)
\( \Rightarrow \widehat C = \widehat {C'}\) (hai góc tương ứng)
Xét hai tam giác vuông \(AHC \) và \(A'H'C'\) có:
\(\widehat {AHC} = \widehat {A'H'C'} = {90^o}\)
\(AC = A’C’\) (chứng minh trên)
\(\widehat C = \widehat {C'}\) (chứng minh trên)
\( \Rightarrow ΔAHC = ΔA'H'C'\) (cạnh huyền – góc nhọn)
\( \Rightarrow AH = A’H’\) (hai cạnh tương ứng).
Bài 5.4
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = AC.\) Lấy điểm \(D\) thuộc cạnh \(AB,\) điểm \(E\) thuộc cạnh \(AC\) sao cho \(AD = AE.\) Đường thẳng đi qua \(D\) và vuông góc với \(BE\) cắt đường thẳng \(CA \) tại \(K.\) Chứng minh rằng \(AK = AC.\)
Phương pháp giải:
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết:
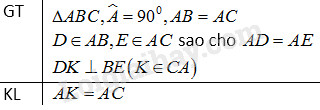
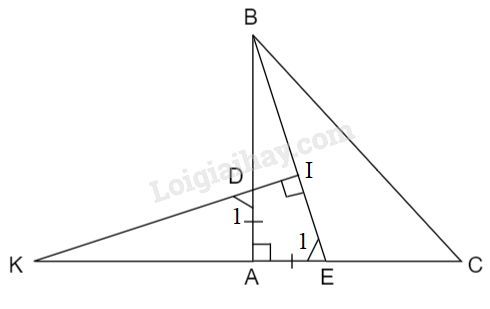
Giả sử đường thẳng đi qua \(D\) và vuông góc với \(BE\) cắt \(BE\) tại \(I\).
Xét tam giác \(ADK\) có \(\widehat {DAK} = {90^o}\)
\( \Rightarrow \widehat {{D_1}} + \widehat K = {90^o}\) (1)
Xét tam giác \(KIE\) có \(\widehat {KIE} = {90^o}\)
\( \Rightarrow \widehat K + \widehat {{E_1}} = {90^o}\) (2)
Từ (1) và (2) suy ra \(\widehat {{D_1}} = \widehat {{E_1}}\).
Xét \(ΔKAD \) và \( ΔBAE\) có:
\(\widehat {{D_1}} = \widehat {{E_1}}\) (chứng minh trên)
\(AD=AE\) (gt)
\(\widehat {KAD} = \widehat {BAE} = {90^o}\)
\( \Rightarrow ΔKAD = ΔBAE\) (g.c.g)
\( \Rightarrow AK = AB.\)
Ta lại có \(AB = AC\) (gt) nên \(AK = AC.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 66 trang 146 SBT toán 7 tập 1
- Bài 65 trang 146 SBT toán 7 tập 1
- Bài 64 trang 146 SBT toán 7 tập 1
- Bài 63 trang 146 SBT toán 7 tập 1
- Bài 62 trang 145 SBT toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
