-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 5 trang 102 SBT toán 7 tập 2
Bài 5 trang 102 sách bài tập toán 7. Cho tam giác ABC vuông góc tại A, phân giác BD. a) So sánh các độ dài AB và AD; b) So sánh các độ dài BC và BD.
Đề bài
Cho tam giác \(ABC\) vuông góc tại \(A, \) phân giác \(BD.\)
a) So sánh các độ dài \(AB\) và \(AD;\)
b) So sánh các độ dài \(BC\) và \(BD.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Trong một tam giác: Góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với đỉnh đó
+) Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn
+) Trong các đường xiên kẻ từ 1 điểm đến 1 đường thẳng: Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Lời giải chi tiết
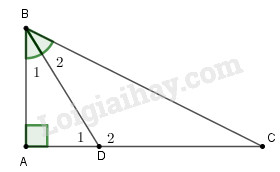
a) Xét tam giác \(BCD\) có \(\widehat {{D_1}}\) là góc ngoài tại đỉnh \(D\) nên \(\widehat {{D_1}} = \widehat {{B_2}} + \widehat C \Rightarrow \widehat {{D_1}} > \widehat {{B_2}}\)
Mà \(\widehat {{B_2}} = \widehat {{B_1}}\) (do \(BD\) là phân giác góc \(B\)) nên \(\widehat {{D_1}} > \widehat {{B_1}}\)
Xét tam giác \(ABD\) có \(\widehat {{D_1}} > \widehat {{B_1}}\) nên \(AB > AD\) (đối diện với góc lớn hơn là cạnh lớn hơn)
b) Cách 1:
Hai đường xiên \(BD,BC\) có hai hình chiểu xuống cạnh \(AC\) là \(AD\) và \(AC.\)
Mà \(AD < AC \Rightarrow BD < BC\) (quan hệ giữa hình chiếu và đường xiên)
Cách 2:
Xét tam giác ABD có là \(\widehat {{D_2}}\) là góc ngoài tam giác tại đỉnh D nên:
\(\widehat {{D_2}} = \widehat {{B_1}} + \widehat A \Rightarrow \widehat {{D_2}} > \widehat {A}\)
Mà \(\widehat {A}=90^0\) nên \(\widehat {{D_2}} > 90^0\) hay \(\widehat {{D_2}} \) là góc tù.
Xét tam giác \(ΔBDC\) có \(\widehat {{D_2}} \) là góc tù nên cạnh đối diện với góc \(\widehat {{D_2}} \) là cạnh lớn nhất trong tam giác, hay BC là cạnh lớn nhất của \(ΔBDC\)
Do đó \(BC > BD.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 6 trang 102 SBT toán 7 tập 2
- Bài 7 trang 102 SBT toán 7 tập 2
- Bài 8* trang 102 SBT toán 7 tập 2
- Bài 9* trang 102 SBT toán 7 tập 2
- Bài 4 trang 102 SBT toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
