Giải bài tập, Sách bài tập (SBT) Toán 7 Bài 6. Tam giác cân

Bài 67 trang 147 SBT toán 7 tập 1


Giải bài 67 trang 147 sách bài tập toán 7 tập 1. a) Tính góc ở đáy của một tam giác cân.

Đề bài

a) Tính góc ở đáy của một tam giác cân biết góc ở đỉnh bằng \({50^o}\), bằng \({a^o}\).

b) Tính góc ở đỉnh của một tam giác cân biết góc ở đáy bằng \({50^o}\), bằng \({a^o}\).

Phương pháp giải - Xem chi tiết

- Tam giác cân có hai góc đáy bằng nhau.

- Tổng ba góc của một tam giác bằng \(180^o\).

Lời giải chi tiết

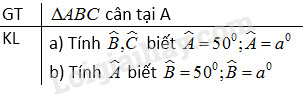
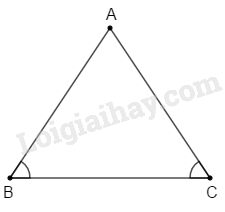
Xét tam giác \(ABC\) cân tại \(A\). 

\( \Rightarrow \widehat B = \widehat C\) (tính chất tam giác cân)

a) Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\) ta có:

\(\widehat A + \widehat B + \widehat C = {180^o}\)

\(\begin{array}{l}
\Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\\\Rightarrow \widehat B +\widehat B= {180^o} - \widehat A\\
\Rightarrow 2\widehat B = {180^o} - \widehat A\\
\Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A}}{2}
\end{array}\)

- Với \(\widehat A = {50^o}\) ta có:

\(\widehat B = \widehat C = \dfrac{{{{180}^o} - {{50}^o}}}{2} = {65^o}\)

- Với \(\widehat A = {a^o}\) ta có:

\(\widehat B = \widehat C = \dfrac{{{{180}^o} - {a^o}}}{2}\)

b) Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\) ta có:

\(\widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat A = {180^o} - \left( {\widehat B + \widehat C} \right)\)

- Với \(\widehat B = \widehat C = {50^o}\) ta có:

\(\widehat A = {180^o} - ({50^o}+50^0) = {80^o}\)

- Với \(\widehat B = \widehat C = {a^o}\) ta có: 

\(\widehat A = {180^o} -(a^0+a^0)= {180^o} - 2.{a^o}\)

Loigiaihay.com

 


Bình chọn:
4.8 trên 16 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store