Bài 6.1, 6.2, 6.3, 6.4, 6.5 phần bài tập bổ sung trang 148, 149 SBT toán 7 tập 1

Bài 6.1

Góc $ADB$ trên hình bs 3 có số đo bằng

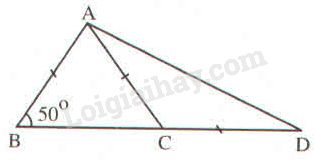
(A) $20^o$;

(B) $25^o$;

(C) $30^o$;

(D) $35^o$;

Hãy chọn phương án đúng. 

Phương pháp giải:

- Tam giác có hai cạnh bằng nhau là tam giác cân.

- Tính chất: Tam giác cân có hai góc ở đáy bằng nhau.

- Định lí: Tổng các góc của một tam giác bằng $180^o$.

Lời giải chi tiết:

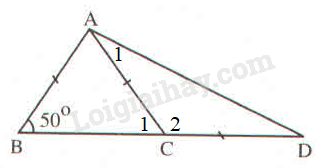
Vì $AB=AC$ (gt) $\Rightarrow \Delta ABC$ cân tại $A$.

$\Rightarrow \widehat B = \widehat {{C_1}} = {50^o}$ (tính chất tam giác cân).

Lại có: $\widehat {{C_1}} + \widehat {{C_2}} = {180^o}$ (hai góc kề bù).

$\begin{array}{l} \Rightarrow \widehat {{C_2}} = {180^o} - \widehat {{C_1}}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^o} - {50^o} = {130^o} \end{array}$

Vì $CA=CD$ (gt) $\Rightarrow \Delta ACD$ cân tại $C$.

$\Rightarrow \widehat {{A_1}} = \widehat D$ (tính chất tam giác cân).

Áp dụng định lí tổng các góc của một tam giác vào $\Delta ACD$, ta có:

$\begin{array}{l} \widehat {{A_1}} + \widehat {{C_2}} + \widehat D = {180^o}\\ \Rightarrow \widehat D + \widehat {{C_2}} + \widehat D = {180^o}\\ \Rightarrow 2\widehat D = {180^o} - \widehat {{C_2}}\\ \Rightarrow \widehat D = \dfrac{{{{180}^o} - \widehat {{C_2}}}}{2}\\ \Rightarrow \widehat D = \dfrac{{{{180}^o} - {{130}^o}}}{2} = {25^o} \end{array}$

Vậy $\widehat {ADB} = {25^o}$. 

Chọn B.

Bài 6.2

Cho tam giác $ABC$ vuông cân tại $A.$ Trên tia đối của tia $BC$ lấy điểm $D$ sao cho $BD = BA.$ Tính số đo góc $ADB$ 

Phương pháp giải:

- Tam giác có hai cạnh bằng nhau là tam giác cân.

- Tính chất: Tam giác cân có hai góc ở đáy bằng nhau.

- Định lí: Tổng các góc của một tam giác bằng $180^o$.

- Trong tam giác vuông hai góc nhọn phụ nhau. 

Lời giải chi tiết:

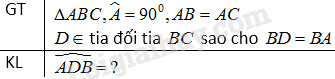
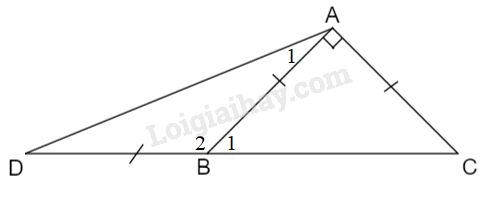
Tam giác $ABC$ vuông cân tại $A$ nên $\widehat {{B_1}} = \widehat C$ (tính chất tam giác cân)   (1)

Ta có: $\widehat {{B_1}} + \widehat C = {90^o}$ (trong tam giác vuông hai góc nhọn phụ nhau)    (2)

Từ (1) và (2) suy ra: $\widehat {{B_1}} = \widehat C = {90^o}:2 = {45^o}$.

Lại có: $\widehat {{B_1}} + \widehat {{B_2}} = {180^o}$ (hai góc kề bù)

$\begin{array}{l} \Rightarrow \widehat {{B_2}} = {180^o} - \widehat {{B_1}}\\ \Rightarrow \widehat {{B_2}} = {180^o} - {45^o} = {135^o} \end{array}$

Vì $BD = BA$ (gt) $\Rightarrow \Delta ABD$ cân tại $B$.

$\Rightarrow \widehat D = \widehat {{A_1}}$ (tính chất tam giác cân).

Áp dụng định lí tổng các góc của một tam giác vào $\Delta ABD$, ta có:

$\begin{array}{l} \widehat {{A_1}} + \widehat {{B_2}} + \widehat D = {180^o}\\ \Rightarrow \widehat D + \widehat {{B_2}} + \widehat D = {180^o}\\ \Rightarrow 2\widehat D + \widehat {{B_2}} = {180^o}\\ \Rightarrow \widehat D = \dfrac{{{{180}^o} - \widehat {{B_2}}}}{2}\\ \Rightarrow \widehat D = \dfrac{{{{180}^o} - {{135}^o}}}{2} = {22^o}30' \end{array}$

Vậy $\widehat {ADB} = {22^o}30'.$

Bài 6.3

Cho tam giác cân $ABC$ có $\widehat A = {100^o}$. Trên cạnh $BC$ lấy điểm $D$ và $E$ sao cho $BD = BA, CE = CA.$ Tính số đo góc $DAE.$

Phương pháp giải:

- Áp dụng kết quả: Một tam giác cân có góc ở đỉnh bằng $a^o$ thì số đo góc ở đáy là $\dfrac{{{{180}^o} - {a^o}}}{2}$

- Định lí tổng ba góc của một tam giác bằng $180^o$.

Lời giải chi tiết:

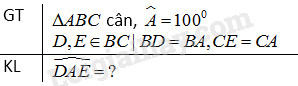
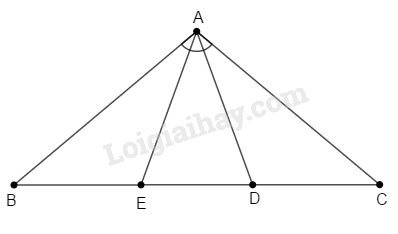
Tam giác $ABC$ cân tại $A$ nên $\widehat B = \widehat C$ (tính chất tam giác cân).

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta ABC$, ta có:

$\begin{array}{l} \widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat A + 2\widehat B = {180^o}\\ \Rightarrow \widehat B = \dfrac{{{{180}^o} - \widehat A}}{2}\\ \Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^o} - {{100}^o}}}{2} = {40^o} \end{array}$

Vì $BD = BA$ (gt) $\Rightarrow \Delta ABD$ cân tại $B$

$\Rightarrow \widehat {ADB} =\widehat {BAD}$

Mà trong tam giác ABD có: $\widehat {ADB} +\widehat {BAD}+\widehat B=180^0$ (định lí tổng ba góc của một tam giác)

$\Rightarrow 2\widehat {ADB}= {180}^o- \widehat B$

$\Rightarrow \widehat {ADB} = \dfrac{{{{180}^o} - \widehat B}}{2}$$\, = \dfrac{{{{180}^o} - {{40}^o}}}{2} = {70^o}$

hay $\widehat {ADE} = {70^o}$

Vì $CE = CA$ (gt) $\Rightarrow \Delta ACE$ cân tại $C$

$\Rightarrow \widehat {AEC} =\widehat {CAE}$

Mà trong tam giác AEC có: $\widehat {AEC} +\widehat {CAE}+\widehat C=180^0$ (định lí tổng ba góc của một tam giác)

$\Rightarrow 2\widehat {AEC}= {180}^o- \widehat C$

$\Rightarrow \widehat {AEC} = \dfrac{{{{180}^o} - \widehat C}}{2}$$\, = \dfrac{{{{180}^o} - {{40}^o}}}{2} = {70^o}$

hay $\widehat {AED} = {70^o}$

Áp dụng định lí tổng các góc của một tam giác vào $\Delta ADE$, ta có:

$\begin{array}{l} \widehat {DAE} + \widehat {ADE} + \widehat {AED} = {180^o}\\ \Rightarrow \widehat {DAE} = {180^o} - \left( {\widehat {ADE} + \widehat {AED}} \right)\\ \Rightarrow \widehat {DAE} = {180^o} - \left( {{{70}^o} + {{70}^o}} \right)\\ \Rightarrow \widehat {DAE} = {40^o} \end{array}$ 

Bài 6.4

Cho hình bs 4. Chứng minh rằng : 

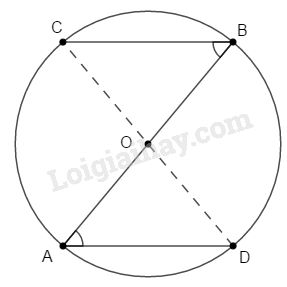
a) $C,O,D$ thẳng hàng ;

b) $BC = AD$. 

Phương pháp giải:

+) Tam giác cân có hai góc ở đáy bằng nhau.

+) $\Delta ABC$ và $\Delta A'B'C'$ có $\widehat A = \widehat {A'};\,\widehat B = \widehat {B'}$ thì $\widehat C = \widehat {C'}.$

Lời giải chi tiết:

a) $OB=OC$ (bằng bán kính đường tròn) $\Rightarrow \Delta BOC$ cân tại $O$.

$\Rightarrow \widehat B = \widehat C$ (tính chất tam giác cân)   (1)

$OA=OD$ (bằng bán kính đường tròn) $\Rightarrow \Delta AOD$ cân tại $O$.

$\Rightarrow \widehat A = \widehat D$ (tính chất tam giác cân)   (2)

Mà $\widehat A = \widehat B$ (gt)   (3)

Từ (1), (2), (3) suy ra $\widehat A = \widehat B = \widehat C = \widehat D$.

Vậy hai tam giác cân $AOD$ và $BOC$ có các góc ở đáy bằng nhau nên góc ở đỉnh cũng bằng nhau.

Suy ra $\widehat {AOD} = \widehat {BOC}$   (4)

Ta có: $\widehat {AOD} + \widehat {DOB} = {180^o}$ (hai góc kề bù)   (5)

Từ (4) và (5) suy ra: $\widehat {BOC} + \widehat {DOB} = {180^o}$ hay $C, O, D$ thẳng hàng.

b) Xét $ΔBOC$ và $ΔAOD$ có:

$OB=OA$ (bằng bán kính đường tròn)

$OC=OD$ (bằng bán kính đường tròn) 

$\widehat {BOC}=\widehat {AOD}$ (chứng minh trên)

$\Rightarrow ΔBOC = ΔAOD$ (c.g.c)

$\Rightarrow  BC = AD$ (hai cạnh tương ứng).

Bài 6.5

Cho tam giác $ABC$ vuông tại $A$, $\widehat B = {30^o}$. Chứng minh rằng $AC = \dfrac{1}{2}BC.$ 

Phương pháp giải:

- Trong tam giác vuông hai góc nhọn phụ nhau.

- Tam giác cân có một góc $60^o$ là tam giác đều.

Lời giải chi tiết:

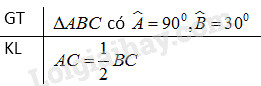
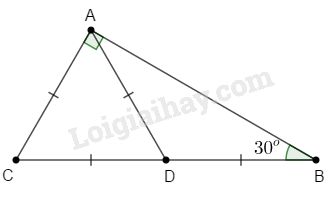
Lấy điểm $D$ trên cạnh $BC$ sao cho $CA=CD$.

Xét tam giác $ABC$ có $\widehat A = {90^o}$

$\Rightarrow \widehat B + \widehat C = {90^o}$ (trong tam giác vuông hai góc nhọn phụ nhau).

$\Rightarrow \widehat C = {90^o} - \widehat B = {90^o} - {30^o} = {60^o}$

Xét tam giác $ACD$ có $CA=CD;\;\widehat C = {60^o}$ nên $\Delta ACD$ là tam giác đều.

$\Rightarrow AC = AD = CD$     (1)

     $\widehat {CAD} = \widehat C = \widehat {ADC} = {60^o}$

Ta có:

$\begin{array}{l} \widehat {CAD} + \widehat {DAB} = {90^o}\\ \Rightarrow \widehat {DAB} = {90^o} - \widehat {CAD}\\ \Rightarrow \widehat {DAB} = {90^o} - {60^o} = {30^o} \end{array}$

Xét $\Delta ABD$ có $\widehat {DAB} = \widehat {ABD} = {30^o}$ nên $\Delta ABD$ là tam giác cân.

$\Rightarrow AD = DB$ (tính chất tam giác cân)   (2)

Từ (1) và (2) suy ra $AC = DC = BD$ hay $AC = \dfrac{1}{2}BC.$

Loigiaihay.com