Bài 8 trang 39 Tài liệu dạy – học Toán 9 tập 2

Giải bài tập a) Vẽ đồ thị (P) của hàm số

Đề bài

a) Vẽ đồ thị (P) của hàm số \(y = {x^2}\) và đường thẳng (d): \(y = 2x+3\) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (d).

Phương pháp giải - Xem chi tiết

Để tìm tọa độ giao điểm của (P) và (d) ta viết phương trình hoành độ giao điểm của (P) và (d) sau đó đi tìm x, từ đó suy ra y.

Lời giải chi tiết

a) Bảng giá trị:

\(x\)	\( - 2\)	\( - 1\)	0	1	2
\(y = {x^2}\)	4	1	0	1	4
\(y = 2x + 3\)		1	3

Vậy đồ thị hàm số \(y = {x^2}\)là 1 Parabol đi qua các điểm có tọa độ là \(\left( { - 2;4} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1;1} \right);\left( {2;4} \right)\)

Đồ thị hàm số \(y = 2x + 3\) là 1 đường thẳng đi qua các điểm có tọa độ là \(\left( { - 1;1} \right);\left( {0;3} \right)\)

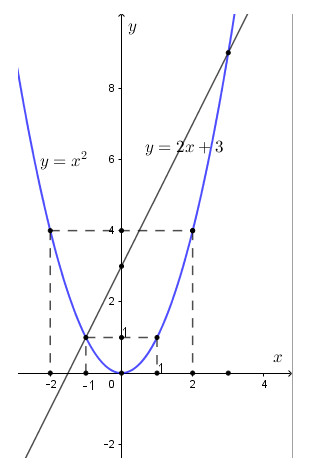
b) Tìm tọa độ giao điểm của (P) và (d).

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình:

\(\begin{array}{l}{x^2} = 2x + 3\\ \Leftrightarrow {x^2} - 2x - 3 = 0\\ \Leftrightarrow {x^2} + x - 3x - 3 = 0\\ \Leftrightarrow x\left( {x + 1} \right) - 3\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right.\end{array}\)

Với \(x = - 1 \Rightarrow y = {\left( { - 1} \right)^2} = 1 \Rightarrow A\left( { - 1;1} \right)\)

Với \(x = 3 \Rightarrow y = {3^2} = 9 \Rightarrow B\left( {3;9} \right)\)

Vậy tọa độ giao điểm của (P) và (d) là: A(-1;1); B(3;9).

Loigiaihay.com