Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 4: Hàm số bậc hai

Bài 15 trang 40 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập a) Vẽ đồ thị (P).

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Đề bài

Cho (P): \(y = \dfrac{{{x^2}}}{4}\) và (D) \(y = -x + 3\)

a) Vẽ đồ thị (P).

b) Viết phương trình đường thẳng (d) song song với (D) và cắt đồ thị (P) tại điểm có hoành độ là -4.

Phương pháp giải - Xem chi tiết

Cho hai đường thẳng \(\left( d \right)y = ax + b;\,\,\,\left( {d'} \right)y = a'x + b'\) . (d) và (d’) song song với nhau khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\)

Lời giải chi tiết

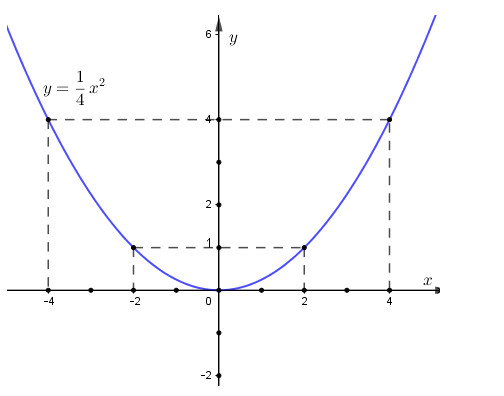
a) Vẽ đồ thị (P).

Bảng giá trị

\(x\)

\( - 4\)

\( - 2\)

0

2

4

\(y = \dfrac{1}{4}{x^2}\)

\(4\)

\(1\)

0

1

4

Vậy đồ thị hàm số \(y = \dfrac{1}{4}{x^2}\) là parabol đi qua các điểm có tọa độ là:\(\left( {-4;4} \right);\left({-2;1} \right);\left({0;0}\right);\left({2;1}\right);\left({4;4}\right)\)

 

b) Viết phương trình đường thẳng (d) song song với (D): \(y = -x + 3\) và cắt đồ thị (P) tại điểm có hoành độ là -4.

Gọi đường thẳng (d) cần tìm có dạng \(y = ax + b\) .

Do (d) song song với (D): \(y = -x + 3\) nên ta có: \(\left\{ \begin{array}{l}a =  - 1\\b \ne 3\end{array} \right.\) . Khi đó (d) có dạng: \(y =  - x + b\,\,\left( {b \ne 3} \right)\)

(d) cắt (P) tại điểm có hoành độ bằng -4 nên  \(x = - 4\) thay vào (P) :\(y = \dfrac{1}{4}{x^2}\) ta được:

\(y = \dfrac{1}{4}.{\left( { - 4} \right)^2} = 4\). Nên điểm có tọa độ \(\left( { - 4;4} \right)\) thuộc đồ thị hàm số (d).

Khi đó thay \(x =  - 4;y = 4\)  vào (d) ta có: \(4 = - \left( { - 4} \right) + b \Leftrightarrow b = 0\left( {tm} \right)\)

Vậy phương trình đường thẳng (d) cần tìm là: \(y =  - x\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com, cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua