Tài liệu Dạy - học Toán 7

Luyện tập - Chủ đề 4: Tam giác cân. Định lý Pythagore

Bài 1 trang 171 Tài liệu dạy – học Toán 7 tập 1

Bình chọn:
4.9 trên 7 phiếu

Giải bài tập Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE.

Xem thêm: Luyện tập - Chủ đề 4: Tam giác cân. Định lý Pythagore

Đề bài

Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE.

a) So sánh \(\widehat {ABD}\)  và \(\widehat {ACE}.\)

b) Gọi I là giao điểm của BD và CE. Tam giác IBC là tam giác gì ? Vì sao ?

Lời giải chi tiết

 

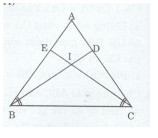
a)Xét tam giác ABD và ACE có:

AB = AC (tam giác ABC cân tại A)

\(\widehat {BAD} = \widehat {CAE}\)   (góc chung)

AD = AE (giả thiết)

Do đó: \(\Delta ABD = \Delta ACE(c.g.c) \Rightarrow \widehat {ABD} = \widehat {ACE}.\)

b) Ta có:

\(\eqalign{  & \widehat {ABD} + \widehat {DBC} = \widehat {ABC}  \cr  & \widehat {ACE} + \widehat {ECD} = \widehat {ACB} \cr} \)

Mà \(\widehat {ABC} = \widehat {ACB}(\Delta ABC\)  cân tại A)

Nên \(\widehat {ABD} + \widehat {DBC} = \widehat {ACE} + \widehat {ECB}\)

Mặt khác: \(\widehat {ABD} = \widehat {ACE}\)   (chứng minh câu a) \(\Rightarrow \widehat {DBC} = \widehat {ECB}.\)   Vậy tam giác BIC cân tại I.

Loigiaihay.com

Bài tiếp theo
Báo lỗi - Góp ý

Các bài liên quan: - Luyện tập - Chủ đề 4: Tam giác cân. Định lý Pythagore

>>Học trực tuyến lớp 7, mọi lúc, mọi nơi môn Toán, Văn, Anh, Lý, Sử cùng các thầy cô giáo dạy giỏi, nổi tiếng.

Các bài khác cùng chuyên mục

Tải app để xem offline!hot

App Loigiaihay trên google play store App Loigiaihay trên apple store

Các tác phẩm khác