Bài 6.1, 6.2, 6.3, 6.4, 6.5, 6.6 phần bài tập bổ sung trang SBT toán 6 tập 2
Giải bài .1 phần bài tập bổ sung trang sách bài tập toán 6 tập 2. Vẽ góc xOy = 50 độ. Vẽ tiếp góc yOz kề bù với góc xOy. Vẽ tiếp Om là tia phân giác của góc xOy. Vẽ tiếp On là tia phân giác của góc yOz ...
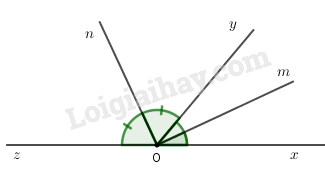
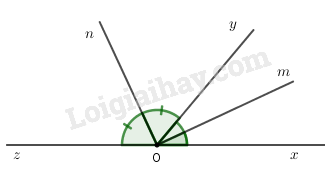
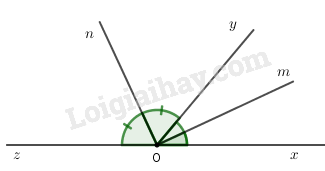
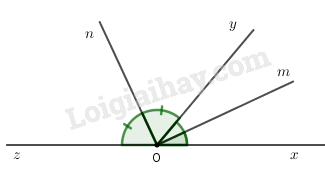
Vẽ \(\widehat {xOy} = 50^\circ \). Vẽ tiếp góc \(yOz\) kề bù với góc \(xOy\). Vẽ tiếp \(Om\) là tia phân giác của góc \(xOy\). Vẽ tiếp \(On\) là tia phân giác của góc \(yOz\).
Dùng giả thiết trên cho các bài số 6.1, 6.2, 6.3, 6.4 sau đây. Hãy chọn kết quả đúng.
Bài 6.3
Số đo của góc \(mOn\) bằng
(A) \(25° ;\) (B) \(65°;\)
(C) \(90°;\) (D) \(115°\)
Bài 6.1
Bài 6.1
Số đo của góc \(xOn\) bằng
(A) \(25° ;\) (B) \(115°;\)
(C) \(90°; \) (D) \(65°\)
Phương pháp giải:
Áp dụng các tính chất :
- Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}.\)
- Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2.\)
- Hai góc kề bù thì có tổng số đo bằng 180 độ.
Lời giải chi tiết:
Vì góc \(yOz\) kề bù với góc \(xOy\) nên \(\widehat {xOy} + \widehat {yOz} =180^\circ\)
\(\Rightarrow \widehat {yOz} =180^\circ - \widehat {xOy}\)\(= 180^\circ - 50^\circ = 130^\circ.\)
Ta có \(On\) là tia phân giác của góc \(yOz\) nên \(\widehat{yOn}= \widehat{zOn}=\dfrac{\widehat{yOz}}{2} = \dfrac{130^\circ}{2} = 65^\circ\)
Ta có : góc \(zOn\) kề bù với góc \(xOn\)
\(\Rightarrow\widehat {xOn} + \widehat {zOn} =180^\circ\)
\(\Rightarrow \widehat {xOn} =180^\circ - \widehat {zOn}\)\(= 180^\circ - 65^\circ = 115^\circ.\)
Chọn đáp án (B) \(115°.\)
Bài 6.2
Bài 6.2
Số đo của góc \(xOm\) bằng
(A) \(25° ;\) (B) \(65°;\)
(C) \( 90°;\) (D) \(115°.\)
Phương pháp giải:
Áp dụng các tính chất :
- Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}.\)
- Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2.\)
- Hai góc kề bù thì có tổng số đo bằng 180 độ.
Lời giải chi tiết:
Vì \(Om\) là tia phân giác của góc \(xOy\) nên ta có :
\(\widehat{xOm}= \widehat{mOy}=\dfrac{\widehat{xOy}}{2} = \dfrac{50^\circ}{2} = 25^\circ\)
Chọn đáp án (A) \(25°.\)
Bài 6.3
Bài 6.3
Số đo của góc \(mOn\) bằng
(A) \(25° ;\) (B) \(65°;\)
(C) \(90°;\) (D) \(115°\)
Phương pháp giải:
Áp dụng các tính chất :
- Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}.\)
- Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2.\)
- Hai góc kề bù thì có tổng số đo bằng 180 độ.
Lời giải chi tiết:
Theo kết quả đã tính ở bài 6.1 và 6.2 ta có:
\(\widehat{yOn} = 65^\circ\) ; \(\widehat{yOm}= 25^\circ.\)
Vì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\)
Lại có tia \(Om\) nằm giữa hai tia \(Ox\) và \(Oy\) (do \(Om\) là phân giác góc \(xOy)\),
tia \(On\) nằm giữa hai tia \(Oz\) và \(Oy\) (do \(On\) là phân giác góc \(zOy)\)
Nên tia \(Oy\) nằm giữa hai tia \(Om\) và \(On\)
Suy ra: \(\widehat{mOn} = \widehat{yOm} + \widehat{yOn}\)\(= 25^\circ + 65^\circ = 90^\circ\)
Chọn đáp án (C) \(90°.\)
Bài 6.4
Bài 6.4
Số đo của góc \(mOz\) bằng
(A) \(25° ;\) (B) \(90°;\)
(C) \(115°; \) (D) \(155°.\)
Phương pháp giải:
Áp dụng các tính chất :
- Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}.\)
- Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2.\)
- Hai góc kề bù thì có tổng số đo bằng 180 độ.
Lời giải chi tiết:
Ta có : góc \(xOm\) kề bù với góc \(mOz\)
\(\Rightarrow\widehat {xOm} + \widehat {mOz} =180^\circ\)
\(\Rightarrow \widehat {mOz} =180^\circ - \widehat {xOm}\)\(= 180^\circ - 25^\circ = 155^\circ.\)
Chọn đáp án (D) \(155°.\)
Bài 6.5
Mỗi câu sau đây là đúng hay sai ?
a) Tia nằm trong góc \(xOy\) là tia phân giác của góc đó;
b) Tia tạo với một cạnh của góc \(xOy\) một góc bằng nửa số đo góc \(xOy\) là tia phân giác của góc đó;
c) Mỗi góc có duy nhất một tia phân giác;
d) Mỗi góc có duy nhất một đường phân giác.
Phương pháp giải:
Dựa vào định nghĩa : Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
Lời giải chi tiết:
Trong bài này chỉ có câu d là đúng, các câu còn lại là sai.
Giải thích:
a) Sai vì thiếu điều kiện tia tạo với hai cạnh Ox, Oy hai góc bằng nhau.
b) Sai vì thiếu điều kiện tia nằm giữa hai cạnh của góc
c) Sai vì góc bẹt có hai tia phân giác là hai tia đối nhau.
d) Đúng
Bài 6.6
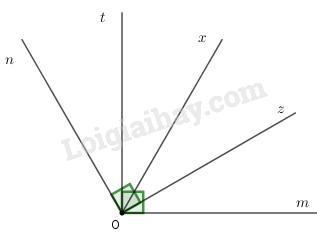
Vẽ \(\widehat {mOn} = 120^\circ \). Vẽ tiếp \(\widehat {mOt} = 90^\circ \) sao cho tia \(Ot\) nằm trong góc \(mOn\). Vẽ tiếp \(\widehat {nOz} = 90^\circ \) sao cho tia \(Oz\) nằm trong góc \(mOn\). Vẽ tiếp \(Ox\) là tia phân giác của góc \(mOn\).
a) Cho biết số đo của góc \(nOt.\)
b) Cho biết số đo của góc \(mOz;\)
c) Cho biết số đo của góc \(zOx.\)
Phương pháp giải:
Áp dụng các tính chất :
- Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}.\)
- Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2.\)
Lời giải chi tiết:
Ta có thể vẽ như hình bs.16
a) Trên nửa mặt phẳng bờ chứa tia \(Om\) có \(\widehat{mOt}< \widehat{mOn}\) (\(90^\circ < 120^\circ\)) nên tia \(Ot\) nằm giữa hai tia \(Om, On\)
\(\Rightarrow \widehat {mOt} + \widehat {nOt} = \widehat {mOn}\)
Thay \(\widehat {mOn} = 120^\circ \) và \(\widehat {mOt} = 90^\circ \) ta có :
\(90^\circ +\widehat {nOt} =120^\circ \)
\(\Rightarrow \widehat {nOt} = 120^\circ - 90^\circ = 30^\circ \).
b) Trên nửa mặt phẳng bờ chứa tia \(On\) có \(\widehat{nOz}< \widehat{mOn}\) (\(90^\circ < 120^\circ\)) nên tia \(Oz\) nằm giữa hai tia \(Om, On\)
\(\Rightarrow \widehat {mOz} + \widehat {nOz} = \widehat {mOn}\)
Thay \(\widehat {mOn} = 120^\circ \) và \(\widehat {nOz} = 90^\circ \) ta có :
\(90^\circ +\widehat {mOz} =120^\circ \)
\(\Rightarrow \widehat {mOz} = 120^\circ - 90^\circ = 30^\circ \).
c) Do \(Ox\) là tia phân giác của góc \(mOn\), nên \(\displaystyle \widehat {{{mOx}}} ={\widehat {{{mOn}}} \over 2} = {{120^\circ } \over 2} = 60^\circ \)
Trên nửa mặt phẳng bờ chứa tia \(Om\) có \(\widehat{mOz}< \widehat{mOx}\) (\(30^\circ < 60^\circ\)) nên tia \(Oz\) nằm giữa hai tia \(Ox, Om\)
Suy ra \(\widehat {mOz} + \widehat {{{zOx}}} = \widehat {{{mOx}}}\)
Hay \(30^\circ + \widehat {{{zOx}}} = 60^\circ \)
Từ đó \(\widehat {{{zOx}}} = 60^0-30^0=30^\circ \)
Loigiaihay.com













Danh sách bình luận