-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 142 trang 97 SBT Toán 8 tập 1
Giải bài 142 trang 97 sách bài tập toán 8. Cho hình bình hành ABCD, các đường chéo cắt nhau ở O. Gọi E, F, G, H theo thứ tự là giao điểm của các đường phân giác của các tam giác AOB, BOC, COD, DOA...
Đề bài
Cho hình bình hành \(ABCD,\) các đường chéo cắt nhau ở \(O.\) Gọi \(E,\, F,\, G,\, H\) theo thứ tự là giao điểm của các đường phân giác của các tam giác \(AOB,\, BOC,\, COD,\, DOA.\) Chứng minh rằng \(EFGH\) là hình thoi.
Phương pháp giải - Xem chi tiết
Chứng minh hình bình hành có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi.
Lời giải chi tiết
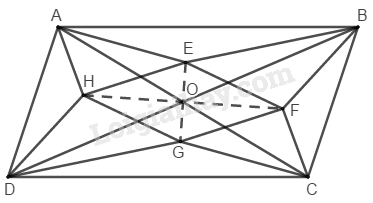
Ta có: \(\widehat {AOB} = \widehat {COD}\) (đối đỉnh)
\(\widehat {EOB} = \displaystyle {1 \over 2}\widehat {AOB}\) (gt)
\(\widehat {COG} = \displaystyle {1 \over 2}\widehat {COD}\) (gt)
Suy ra: \(\widehat {EOB} = \widehat {COG}\)
\(\widehat {EOB} + \widehat {BOC} + \widehat {COG} \)\(= 2\widehat {EOB} + \widehat {BOC}\)
mà \(\widehat {AOB} + \widehat {BOC} = {180^0}\) (kề bù)
hay \(2\widehat {EOB} + \widehat {BOC} = {180^0}\)
Suy ra: \(E,\, O,\, G\) thẳng hàng
Ta lại có: \(\widehat {BOC} = \widehat {AOD}\) (đối đỉnh)
\(\widehat {HOD} = \displaystyle {1 \over 2}\widehat {AOD}\) (gt)
\(\widehat {FOC} = \displaystyle {1 \over 2}\widehat {BOC}\) (gt)
Suy ra: \(\widehat {HOD} = \widehat {FOC}\)
\(\widehat {HOD} + \widehat {COD} + \widehat {FOC}\)\( = 2\widehat {HOD} + \widehat {COD}\)
mà \(\widehat {AOD} + \widehat {COD} = {180^0}\) (kề bù)
hay \(2\widehat {HOD} + \widehat {COD} = {180^0}\)
Suy ra: \(H,\, O,\, F\) thẳng hàng
\(\widehat {ADO} = \widehat {CBO}\) (so le trong)
\(\widehat {HDO} = \displaystyle {1 \over 2}\widehat {ADO}\) (gt)
\(\widehat {FBO} = \displaystyle {1 \over 2}\widehat {CBO}\) (gt)
Suy ra: \(\widehat {HDO} = \widehat {FBO}\)
- Xét \(∆ BFO\) và \(∆ DHO:\)
\(\widehat {HDO} = \widehat {FBO}\) (chứng minh trên)
\(OD = OB\) (tính chất hình bình hành)
\(\widehat {HOD} = \widehat {FOB}\) (đối đỉnh)
Do đó: \(∆ BFO = ∆ DHO \,(g.c.g)\)
\(⇒ OF = OH\)
\(\widehat {OAB} = \widehat {OCD}\) (so le trong)
\(\widehat {OAE} = \displaystyle {1 \over 2}\widehat {OAB}\) (gt)
\(\widehat {OCG} = \displaystyle {1 \over 2}\widehat {OCD}\) (gt)
Suy ra: \(\widehat {OAE} = \widehat {OCG}\)
- Xét \(∆ OAE\) và \(∆ OCG:\)
\(\widehat {OAE} = \widehat {OCG}\) (chứng minh trên)
\(OA = OC\) (tính chất hình bình hành)
\(\widehat {EOA} = \widehat {GOC}\) (đối đỉnh)
Do đó: \(∆ OAE = ∆ OCG \,(g.c.g)\)
\(⇒ OE = OG\)
Suy ra: Tứ giác \(EFGH\) là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có OE là tia phân giác góc AOB và OF là tia phân giác góc BOC
Mà hai góc AOB và BOC kề bù
Nên \(OE ⊥ OF\) (tính chất hai tia phân giác của hai góc kề bù thì vuông góc với nhau)
hay \(EG ⊥ FH\)
Vậy: Tứ giác \(EFGH\) là hình thoi.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 143 trang 97 SBT Toán 8 tập 1
- Bài 11.1 phần bài tập bổ sung trang 97 SBT Toán 8 tập 1
- Bài 11.2 phần bài tập bổ sung trang 97 SBT Toán 8 tập 1
- Bài 11.3 phần bài tập bổ sung trang 98 SBT Toán 8 tập 1
- Bài 141 trang 97 SBT Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
