 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 2. Đường kính và dây của đường tròn
Bài 2. Đường kính và dây của đường tròn
Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 2 - Hình học 9
Đề bài
Cho đường tròn (O) đường kính \(AB = 2R\). Một dây CD không đi qua tâm O sao cho \(\widehat {COD} = 90^\circ \) và CD cắt đường thẳng AB tại E (D nằm giữa hai điểm E và C), biết \(OE = 2R\). Tính độ dài EC và ED theo R.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
- Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
- Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
Lời giải chi tiết
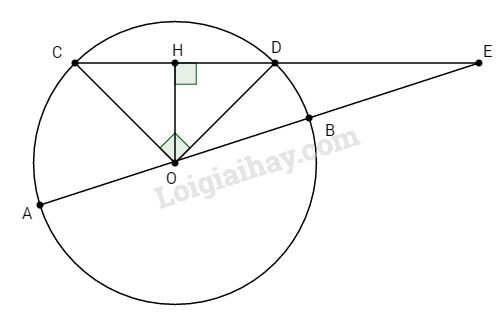
Ta có: \(\widehat {COD} = 90^\circ \) (gt) và OC=OD=R nên ∆COD vuông cân tại O, ta có:
\(CD = \sqrt {O{C^2} + O{D^2}} = \sqrt {2{R^2}} = R\sqrt 2 \)
Kẻ \(OH ⊥ CD\), ta có: \(HC = HD\) (định lí đường kính dây cung)
Mặt khác ∆COD vuông cân nên OH đồng thời là trung tuyến:
\(HC = HD = OH = {{CD} \over 2} = {{R\sqrt 2 } \over 2}\)
Xét tam giác vuông OHE, ta có:
\(EH = \sqrt {O{E^2} - O{H^2}} \) (định lí Pi-ta-go)
\(\eqalign{ & EH = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {{{R\sqrt 2 } \over 2}} \right)}^2}} \cr&\;\;\;\;\;\;\;= {{R\sqrt {14} } \over 2} \cr & \Rightarrow ED = EH - HD \cr&\;\;\;\;\;\;\;\;\;\,\;\;= {{R\sqrt {14} } \over 2} - {{R\sqrt 2 } \over 2}\cr& \;\;\;\;\;\;\;\;\;\;\;\,= {{R\sqrt {14} - R\sqrt 2 } \over 2} \cr & EC = EH + HC = {{R\sqrt {14} + R\sqrt 2 } \over 2} \cr} \)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận