 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 3. Đồ thị của hàm số y = ax + b (a ≠ 0)
Bài 3. Đồ thị của hàm số y = ax + b (a ≠ 0)
Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 2 - Đại số 9
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 2 - Đại số 9
Đề bài
Bài 1. Vẽ đồ thị của hàm số \(y = 3x + 2.\)
Bài 2. Cho hàm số \(y = \left( {m - 2} \right)x + m.\) Tìm m để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 3.
Bài 3. Chứng tỏ rằng họ đường thằng (d) : \(y = \left( {m - 1} \right)x + m\) luôn qua điểm \(A(-1; 1)\) với mọi giá trị m \((m ≠ 1)\)
Bài 4. Cho hàm số \(y = (2m – 1 )x + m\). Tìm m để đồ thị hàm số qua gốc tọa độ.
LG bài 1
Phương pháp giải:
Cách vẽ đồ thị của hàm số \(y = ax + b (a ≠ 0).\)
- Chọn điểm \(P(0; b)\) (trên trục \(Oy\)).
- Chọn điểm \(Q\left( { - \dfrac{b}{a};0} \right)\) (trên trục \(Ox\)).
- Kẻ đường thẳng \(PQ\) ta được đồ thị của hàm số \(y=ax+b.\)
Lời giải chi tiết:
Bảng giá trị:
|
x |
0 |
-1 |
|
y=3x+2 |
2 |
-1 |
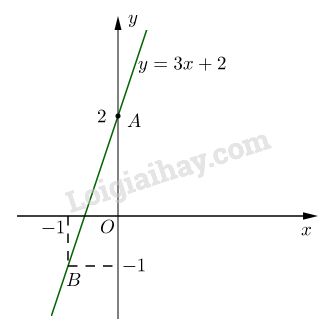
Đồ thị hàm số \(y = 3x + 2\) là đường thẳng qua hai điểm \(A(0; 2)\) và \(B(-1; -1)\).
LG bài 2
Phương pháp giải:
Đường thẳng \(y=ax+b\) có tung độ gốc là \(b\)
Lời giải chi tiết:
Theo giả thiết ta suy ra tung độ gốc của đường thẳng là \(3\) nên ta có \(m = 3\)
LG bài 3
Phương pháp giải:
Thay \(x=-1;y=1\) vào phương trình đường thẳng \((d):y = \left( {m - 1} \right)x + m\) để có 1 hệ thức đúng.
Lời giải chi tiết:
Thay \(x=-1;y=1\) vào phương trình đường thẳng \((d):y = \left( {m - 1} \right)x + m\) ta được: \( 1 = \left( {m - 1} \right).\left( { - 1} \right) + m\) hay \(1 = - m + 1 + m \Leftrightarrow 1 = 1\) luôn đúng với mọi \(m \;(m ≠ 1)\)
Vậy họ đường thằng (d) : \(y = \left( {m - 1} \right)x + m\) luôn qua điểm \(A(-1; 1)\) với mọi giá trị m \((m ≠ 1)\)
LG bài 4
Phương pháp giải:
Thay \(x=0;y=0\) vào hàm số \(y = (2m – 1 )x + m\) để tìm \(m\)
Lời giải chi tiết:
Theo giả thiết, thay \(x=0;y=0\) vào hàm số \(y = (2m – 1 )x + m\) ta có: \(0 = (2m – 1).0 + m ⇒ m = 0\).
Vậy \(m=0.\)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận