-
CHƯƠNG 1. SỐ HỮU TỈ - SỐ THỰC
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC – ĐƯỜNG THẲNG SONG SONG
-
CHƯƠNG 2. TAM GIÁC
-
Chủ đề 3: Tam giác - Tam giác bằng nhau
- 1. Tổng ba góc trong một tam giác
- 2. Hai tam giác bằng nhau
- 3. Trường hợp bằng nhau thứ nhất của tam giác: Cạnh - cạnh - cạnh (c.c.c)
- 4. Trường hợp bằng nhau thứ hai của tam giác: Cạnh - góc - cạnh (c.g.c)
- 5. Trường hợp bằng nhau thứ ba của tam giác: Góc - góc - góc (g.g.g)
- Bài tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
- Luyện tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
-
Chủ đề 4. Tam giác cân - Định lý Pythagore
-
Ôn tập chương 2 - Hình học 7
-
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4. BIỂU THỨC ĐẠI SỐ
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC – CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
-
Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- 1. Quan hệ giữa góc và cạnh trong một tam giác
- 2. Quan hệ giữa đường vuông góc và đường xiên – Giữa đường xiên và hình chiếu
- 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- Luyện tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
-
Chủ đề 6 : Các đường đồng quy của tam giác
- 1. Tính chất ba đường trung tuyến của tam giác
- 2. Tính chất tia phân giác của một góc
- 3. Tính chất ba đường phân giác của tam giác
- 4. Tính chất đường trung trực của một đoạn thẳng
- 5. Tính chất ba đường trung trực của tam giác
- 6. Tính chất ba đường cao trong tam giác
- Bài tập - Chủ đề 6 : Các đường đồng quy của tam giác
- Luyện tập - Chủ đề 6 : Các đường đồng quy của tam giác
-
Ôn tập chương 3 – Hình học
-
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
Bài tập - Chủ đề 1: Góc tạo bởi các đường thẳng
Bài tập 12 trang 116 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Vẽ hai đường thẳng cắt nhau só cho trong các góc tạo thành có một cặp góc đối đỉnh có tổng số đo bằng 130o. Tính số đo mỗi góc có trên hình.
Đề bài
Vẽ hai đường thẳng cắt nhau só cho trong các góc tạo thành có một cặp góc đối đỉnh có tổng số đo bằng 130o. Tính số đo mỗi góc có trên hình.
Phương pháp giải - Xem chi tiết
2 góc kề bù có tổng số đo là \(180^0\)
Lời giải chi tiết
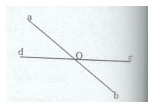
Theo đầu bài ta có: \(\widehat {aOd}\) và \(\widehat {bOc}\) đối đỉnh và \(\widehat {aOd} + \widehat {bOc} = {130^0}.\)
Ta có: \(\widehat {aOd} = \widehat {bOc}\) (hai góc đối đỉnh) nên \(2.\widehat {aOd} = {130^0} \Rightarrow \widehat {aOd} = {130^0}:2 = {65^0}\)
Do đó: \(\widehat {bOc} = \widehat {aOd} = {65^0}\)
Mà \(\widehat {aOd} + \widehat {aOc} = {180^0}\) (kề bù).
Nên \({65^0} + \widehat {aOc} = {180^0} \Rightarrow \widehat {aOc} = {180^0} - {65^0} = {115^0}.\)
\(\widehat {bOd} = \widehat {aOc}\) (hai góc đối đỉnh) nên \(\widehat {bOd} = {115^0}.\)
Ta còn có: \(\widehat {aOb} = {180^0},\widehat {cOd} = {180^0}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 13 trang 116 Tài liệu dạy – học Toán 7 tập 1
- Bài tập 14 trang 116 Tài liệu dạy – học Toán 7 tập 1
- Bài tập 15 trang 116 Tài liệu dạy – học Toán 7 tập 1
- Bài tập 16 trang 116 Tài liệu dạy – học Toán 7 tập 1
- Bài tập 17 trang 116 Tài liệu dạy – học Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
