Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 64 trang 92 SGK Toán 9 tập 2


Trên đường tròn bán kính

Đề bài

Trên đường tròn bán kính \(R\) lần lượt đặt theo cùng một chiều, kể từ điểm \(A\), ba cung \(\overparen{AB}\), \(\overparen{BC}\), \(\overparen{CD}\) sao cho: \(sđ\overparen{AB}\)=\(60^0\), \(sđ\overparen{BC}\)=\(90^0\), \(sđ\overparen{CD}\)=\(120^0\)

a) Tứ giác \(ABCD\) là hình gì?

b) Chứng minh hai đường chéo của tứ giác \(ABCD\) vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác \(ABCD\) theo \(R\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Dựa vào các dấu hiệu nhận biết của các hình tứ giác đặc biệt và các tứ giác nào có thể nội tiếp đường tròn để chứng minh tứ giác ABCD là hình gì.

Chú ý rằng: Hình thang nội tiếp được đường tròn là hình thang cân.

b) Số đo của góc có đỉnh nằm trong đường tròn bằng nửa số đo của tổng hai cung bị chắn.

c) Sử dụng định lý : "Số đo góc nội tiếp bằng nửa số đo cung bị chắn."

Sử dụng định lý Pytagoo để tính toán.

Lời giải chi tiết

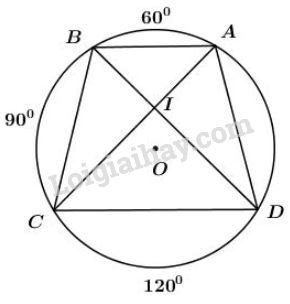
a) Xét đường tròn \((O)\) ta có:

\(\displaystyle \widehat {BA{\rm{D}}} = {{{{90}^0} + {{120}^0}} \over 2} = {105^0}\) (góc nội tiếp chắn \(\overparen{BCD}\))     (1)

\(\displaystyle \widehat {A{\rm{D}}C} = {{{{60}^0} + {{90}^0}} \over 2} = {75^0}\) ( góc nội tiếp chắn \(\overparen{ABC}\) )          (2)

Từ (1) và (2) có:

\(\widehat {BA{\rm{D}}} + \widehat {A{\rm{D}}C} = {105^0} + {75^0} = {180^0}\) (3)

Mà hai góc này ở vị trí trong cùng phía 

Nên \(AB // CD\). Do đó tứ giác \(ABCD\) là hình thang, mà hình thang nội tiếp đường tròn là hình thang cân. 

Vậy \(ABCD\) là hình thang cân suy ra (\(BC = AD\) và \(sđ\overparen{BC}\)=\(sđ\overparen{AD}\)=\(90^0\))

b) Giả sử hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(I\).

\(\widehat {CI{\rm{D}}}\) là góc có đỉnh nằm trong đường tròn, nên:

\(\displaystyle \widehat {CI{\rm{D}}}\) \(=\dfrac{sđ\overparen{AB}+sđ\overparen{CD}}{2}\)\(=\displaystyle {{{{60}^0} + {{120}^0}} \over 2} = {90^0}\)

Vậy \(AC \bot BD.\) 

c) Vì \(sđ\overparen{AB}= 60^0\) nên \(\widehat {AOB} = {60^0}\) (góc ở tâm)

\(=> ∆AOB\) đều, nên \(AB = OA = OB = R.\)

Vì  \( sđ \overparen{BC} = {90^0} \Rightarrow \widehat {BOC} = {90^0}\) (góc ở tâm)

\(\Rightarrow BC = \sqrt{OB^2+OC^2}=R\sqrt2.\)

Kẻ \(OH \bot CD.\)

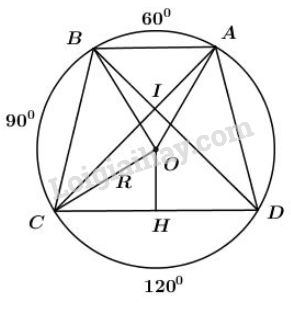
Tứ giác \(ABCD\) là hình thang cân \(\Rightarrow \widehat{BCD}=\widehat{ADC}=75^0.\)

Lại có \(\Delta BOC\) vuông cân tại \(O \Rightarrow \widehat{BCO}=45^0.\)

\(\Rightarrow \widehat{OCD}=\widehat{BCD}-\widehat{BCO}=75^0-45^0=30^0.\)

Xét \(\Delta OCH\) vuông tại \(H\) ta có:

\(HC=OC.\cos \widehat{OCH}=\dfrac{R\sqrt{3}}{2}.\)

Mà \(H\) là trung điểm của \(CD\) (định lý đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy).

\(\Rightarrow CD=2.CH=R\sqrt3.\) 

Loigiaihay.com


Bình chọn:
4.3 trên 77 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store