 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
Bài 63 trang 92 SGK Toán 9 tập 2
Vẽ các hình lục giác đều
Đề bài
Vẽ các hình lục giác đều, hình vuông, hình tam giác đều cùng nội tiếp đường tròn \((O;R)\) rồi tính cạnh của các hình đó theo \(R\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Sử dụng compa và thước kẻ có chia độ dài để vẽ hình.
+) Sử dụng định lý Pi-ta-go để tính R.
Lời giải chi tiết
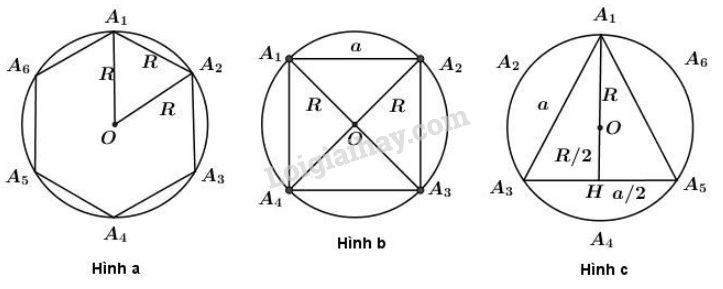
+) Hình a.
Cách vẽ: vẽ đường tròn \((O;R)\). Trên đường tròn ta đặt liên tiếp các cung \(\overparen{{A_1}{A_2}}\), \(\overparen{{A_2}{A_3}}\),...,\(\overparen{{A_6}{A_1}}\) mà dây căng cung có độ dài bằng \(R\). Nối \({A_1}\) với \({A_2}\), \({A_2}\) với \({A_3}\),…, \({A_6}\) với \({A_1}\) ta được hình lục giác đều \({A_1}\)\({A_2}\)\({A_3}\)\({A_4}\)\({A_5}\)\({A_6}\) nội tiếp đường tròn
Tính bán kính:
Gọi \({a_i}\) là cạnh của đa giác đều có \(i\) cạnh.
\({a_6}= R\) (vì \(O{A_1}{A_2}\) là tam giác đều)
+) Hình b.
Cách vẽ:
+ Vẽ đường kính \(A_1A_3\) của đường tròn tâm O.
+ Vẽ đường kính \(A_2A_4 ⊥A_1A_3\)
Tứ giác \(A_1A_2A_3A_4\) có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên là hình vuông.
Nối \(A_1\) với \(A_2;A_2\) với \(A_3;A_3\) với \(A_4;A_4\) với \(A_1\) ta được hình vuông \(A_1A_2A_3A_4\) nội tiếp đường tròn (O).
Tính bán kính:
Gọi độ dài cạnh của hình vuông là \(a.\)
Vì hai đường chéo của hình vuông vuông góc với nhau nên xét tam giác vuông \(O{A_1}{A_2}\) có
\({a^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow a = R\sqrt 2 \)
+) Hình c:
Cách vẽ như câu a) hình a.
Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác \({A_1}{A_3}{A_5}\) như trên hình c.
Tính bán kính:
Gọi độ dài cạnh của tam giác đều là \(a.\)
\({A_1}H\) \(=A_1O+OH= R+\dfrac{R}{2}\) = \(\dfrac{3R}{2}\)
\({A_3}H\) \(= \dfrac{AA'}{2}=\dfrac{a}{2}\)
\({A_1}\)\({A_3}=a\)
Trong tam giác vuông \({A_1}H{A_3}\) ta có: \({A_1}{H^2} = {A_1}{A_3}^2 - {A_3}{H^2}\).
Từ đó \(\dfrac{9R^{2}}{4}\) = \(a^2\) - \(\dfrac{a^{2}}{4}\).
\(\Rightarrow{a^2} = 3{R^2} \Rightarrow a = R\sqrt 3 \)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận