-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Bài 46 trang 11 SBT Hình học 12 Nâng cao
Giải bài 46 trang 11 sách bài tập Hình học 12 Nâng cao. Cho khối lập phương ABCD.A’B’C’D’ cạnh a...
Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’.
LG a
Dựng thiết diện của khối lập phương khi cắt bởi \(mp\left( {AEF} \right).\)
Lời giải chi tiết:
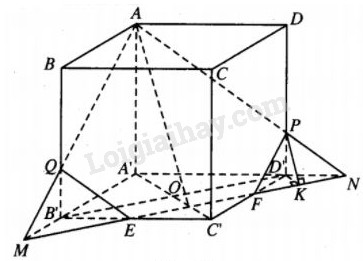
Đường thẳng EF cắt A’D’ tại N, cắt A’B’ tại M, AN cắt DD’ tại P, AM cắt BB’ tại Q.
Vậy thiết diện là ngũ giác APFEQ.
LG b
Tính tỉ số thể tích hai phần của khối lập phương bị chia bởi mặt phẳng \(\left( {AEF} \right).\)
Lời giải chi tiết:
Đặt :
\(\eqalign{ & V = {V_{ABCD.A'B'C'D'}}, \cr & {V_1} = {V_{ABCDC'QEFP}}, \cr & {V_2} = {V_{AQEFP.B'A'D'}}, \cr & {V_3} = {V_{A.MA'N}}, \cr & {V_4} = {V_{PFD'N}},{V_5} = {V_{QMB'E}}. \cr} \)
Dễ thấy \({V_4} = {V_5}\) ( do tính đối xứng của hình lập phương),
\(\eqalign{ & {V_3} = {1 \over 6}AA'.A'M.A'N = {1 \over 6}a.{{3a} \over 2}.{{3a} \over 2} = {{3{a^3}} \over 8}, \cr & {V_4} = {1 \over 6}PD'.D'F.D'N = {1 \over 6}.{a \over 3}.{a \over 2} .{a \over 2} = {{{a^3}} \over {72}}, \cr & {V_2} = {V_3} - 2{V_4} = {{3{a^3}} \over 8} - {{2{a^3}} \over {72}} = {{25{a^3}} \over {72}}, \cr & {V_1} = V - {V_2} = {a^3} - {{25{a^3}} \over {72}} = {{47} \over {72}}{a^3}. \cr} \)
Mặt phẳng \(\left( {AEF} \right)\) chia khối lập phương thành hai phần lần lượt có thể tích là \({V_1} = {{47} \over {72}}{a^3},{V_2} = {{25{a^3}} \over {72}}.\)
Vậy : \({{{V_1}} \over {{V_2}}} = {{47} \over {25}}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 47 trang 11 SBT Hình học 12 Nâng cao
- Bài 48 trang 11 SBT Hình học 12 Nâng cao
- Bài 49 trang 11 SBT Hình học 12 Nâng cao
- Bài 50 trang 11 SBT Hình học 12 Nâng cao
- Bài 51 trang 12 SBT Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
