Giải SBT toán hình học và giải tích 12 nâng cao Bài 4: Thể tích của khối đa diện

Bài 39 trang 10 SBT Hình học 12 Nâng cao


Giải bài 39 trang 10 sách bài tập Hình học 12 Nâng cao. Cho khối chóp S.ABCD ...

Đề bài

Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và SA=2a. Gọi B’, D’ lần lượt là hình chiếu của A trên SB và SD. Mặt phẳng \(\left( {AB'D'} \right)\) cắt SC tại C’. Tính thể tích khối chóp S.AB’C’D’.

Lời giải chi tiết

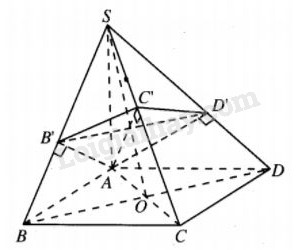
Ta có\(AB' \bot SB,AB' \bot CB(\) do \(CB \bot \left( {SAB} \right)\))

\( \Rightarrow AB' \bot \left( {SBC} \right) \Rightarrow AB' \bot SC   \;\;(1)\)

Tương tự \(AD' \bot SC\;\;\;(2)\)

Từ (1) và (2) suy ra

 \(\eqalign{  & SC \bot \left( {AB'C'D'} \right)  \cr  &  \Rightarrow SC \bot AC'. \cr} \)

Do tính đối xứng ta có

\({V_{S.AB'C'D'}} = 2{V_{S.AB'C'}}\)

Ta có

\(\eqalign{  & {{{V_{S.AB'C'}}} \over {{V_{S.ABC}}}} = {{SB'} \over {SB}}.{{SC'} \over {SC}} = {{SB'.SB} \over {S{B^2}}}.{{SC'.SC} \over {S{C^2}}}    \cr  &  = {{S{A^2}} \over {S{B^2}}}.{{S{A^2}} \over {S{C^2}}} = {{4{a^2}} \over {5{a^2}}}.{{4{a^2}} \over {6{a^2}}} = {8 \over {15}}.  \cr  & {V_{S.ABC}} = {1 \over 3}.{{{a^2}} \over 2}.2a = {{{a^3}} \over 3}\cr& \Rightarrow {V_{S.AB'C'}} = {8 \over {15}}.{{{a^3}} \over 3} = {{8{a^3}} \over {45}}  \cr  &  \Rightarrow {V_{S.AB'C'D'}} = {{16{a^3}} \over {45}}. \cr} \)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store