Giải SBT toán hình học và giải tích 12 nâng cao Bài 4: Thể tích của khối đa diện

Bài 35 trang 10 SBT Hình học 12 Nâng cao


Giải bài 35 trang 10 sách bài tập Hình học 12 Nâng cao. Cho khối chóp tứ giác đều ...

Đề bài

Cho khối chóp tứ giác đều S.ABCD mà khoảng cách từ đỉnh A đến \(mp\left( {SBC} \right)\) bằng 2a. Với giá trị nào của góc giữa mặt bên và mặt đáy của khối chóp thì thể tích của khối chóp là nhỏ nhất ?

Lời giải chi tiết

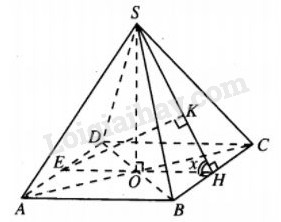
Giả sử O là tâm của hình vuông ABCD. Khi đó \(SO \bot \left( {ABCD} \right)\).

Gọi EH là đường trung bình của hình vuông ABCD \(\left( {E \in AD,H \in BC} \right).\)

Vì \(AD//BC\) nên \(AD//\left( {SBC} \right)\), do đó

\(d\left( {A,\left( {SBC} \right)} \right) = d\left( {E,\left( {SBC} \right)} \right)\)

Kẻ \(EK \bot SH\). Dễ thấy \(EK \bot \left( {SBC} \right)\) suy ra

\(EK = d\left( {A,\left( {SBC} \right)} \right) = 2a.\)

Ta có : \(BC \bot SH,BC \bot OH \Rightarrow \)\(\widehat {SHO}\) là góc giữa mặt bên \(\left( {SBC} \right)\) và mặt phẳng đáy. Đặt \(\widehat {SHO}  =x\left( {0 < x < {\pi  \over 2}} \right)\). Khi đó :

\(EH = {{2a} \over {{\mathop{\rm sinx}\nolimits} }};\;OH = {a \over {{\mathop{\rm s}\nolimits} {\rm{inx}}}};\;SO = {a \over {{\mathop{\rm s}\nolimits} {\rm{inx}}}}{\mathop{\rm tanx}\nolimits}  = {a \over {{\mathop{\rm cosx}\nolimits} }}\)

Vậy: \({V_{S.ABCD}} = {1 \over 3}{S_{ABCD}}.SO = {{4{a^3}} \over {3\cos x{{\sin }^2}x}}\)

Từ đó \({V_{S.ABCD}}\) nhỏ nhất khi và chỉ khi \(y\left( x \right) = \cos x.{\sin ^2}x\) đạt giá trị lớn nhất. Ta có:

\(\eqalign{
 y'\left( x \right) &= - {\sin ^3}x + 2\sin x.{\cos ^2}x \cr 
& = \sin x\left( {2{{\cos }^2}x - {{\sin }^2}x} \right) \cr 
& = \sin x\left( {2 - 3{{\sin }^2}x} \right) \cr 
& = 3\sin x\left( {\sqrt {{2 \over 3}} - \sin x} \right)\left( {\sqrt {{2 \over 3}} + \sin x} \right) \cr} \)

Vì \(0 < x < {\pi  \over 2}\) nên \(\sin x\left( {\sqrt {{2 \over 3}}  + \sin x} \right) > 0\)

Gọi \(\alpha \) là góc sao cho \(\sin \alpha  = \sqrt {{2 \over 3}} ;\,\,0 < \alpha  < {\pi  \over 2}\)

Ta có bảng biến thiên của hàm số \(y\left( x \right) = \cos x.{\sin ^2}x\):

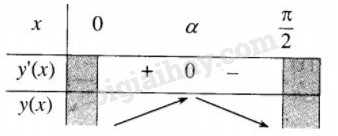
Vậy \({V_{S.ABCD}}\) đạt giá trị lớn nhất khi \(x = \alpha \) với \(0 < \alpha  < {\pi  \over 2}\) và \(\sin x = \sqrt {{2 \over 3}} .\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store