-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Bài 23 trang 9 SBT Hình học 12 Nâng cao
Giải bài 23 trang 9 sách bài tập Hình học 12 Nâng cao. Cho khối lăng trụ tứ giác đều ABCD.A1B1C1D1 ...
Cho khối lăng trụ tứ giác đều ABCD.A1B1C1D1 có khoảng cách giữa hai đường thẳng AB và A1D bằng 2 và độ dài đường chéo của mặt bên bằng 5.
LG a
Hạ \(AK \bot {A_1}D\left( {K \in {A_1}D} \right)\). Chứng minh rằng AK=2.
Lời giải chi tiết:
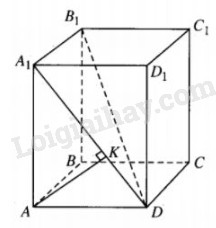
\(\eqalign{ & AB//{A_1}{B_1} \Rightarrow AB// \left( {{A_1}{B_1}D} \right) \cr & \Rightarrow {d_{\left( {A,\left( {{A_1}{B_1}D} \right)} \right)}} = {d_{\left( {AB,{A_1}D} \right)}}. \cr} \)
Ta có :
\(\eqalign{ & {A_1}{B_1} \bot \left( {A{A_1}{D_1}D} \right) \cr & \Rightarrow {A_1}{B_1} \bot AK. \cr} \)
Mặt khác \({A_1}D \bot AK,\) suy ra \(AK \bot \left( {{A_1}{B_1}D} \right)\)
Vậy \(AK = d\left( {A,\left( {{A_1}{B_1}D} \right)} \right)\)\( = d\left( {AB,{A_1}D} \right) = 2\)
LG b
Tính thể tích khối lăng trụ ABCD.A1B1C1D1.
Lời giải chi tiết:
Xét tam giác vuông \({A_1}AD\), ta có :
\(A{K^2} = {A_1}K.KD.\)
Đặt A1K = x \(4 = x\left( {5 - x} \right) \Rightarrow {x^2} - 5x + 4 = 0 \)
\(\Rightarrow \left[ \matrix{ x = 1 \hfill \cr x = 4 \hfill \cr} \right.\)
Với x=1, \(AD = \sqrt {A{K^2} + K{D^2}} = 2\sqrt 5 \)
\({\rm{A}}{{\rm{A}}_1} = \sqrt {{A_1}{D^2} - A{D^2}} = \sqrt 5 \)
Khi đó \({V_{ABCD.{A_1}{B_1}{C_1}{D_1}}} = 20\sqrt 5 \)
Với x=4, tương tự ta có :\({V_{ABCD.{A_1}{B_1}{C_1}{D_1}}} = 10\sqrt 5 \).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 24 trang 9 SBT Hình học 12 Nâng cao
- Bài 25 trang 9 SBT Hình học 12 Nâng cao
- Bài 26 trang 9 SBT hình học 12 nâng cao
- Bài 27 trang 9 SBT Hình học 12 Nâng cao
- Bài 28 trang 9 SBT Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
