Bài 39 trang 129 SGK Toán 9 tập 2

Một hình chữ nhật ABCD có AB > AD, diện tích và chu vi của nó theo thứ tự là 2a2 và 6a.

Đề bài

Một hình chữ nhật \(ABCD\) có \(AB > AD\), diện tích và chu vi của nó theo thứ tự là \(2a^2\) và \(6a\). Cho hình vẽ quay xung quanh cạnh \(AB\), ta được một hình trụ.

Tính diện tích xung quanh và thể tích của hình trụ này.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+) Quay hình chữ nhật quanh một cạnh cố định của nó ta được một hình trụ.

+) Chu vi hình chữ nhật có kích thước \(a, \, b\) là: \(C=2(a+b).\)

+) Diện tích hình chữ nhật có kích thước \(a, \, b\) là: \(S=ab.\)

+) Diện tích xung quanh của hình trụ: \(S_{xq}=2\pi rh.\)

+) Thể tích hình trụ là: \(V=\pi r^2h.\)

Lời giải chi tiết

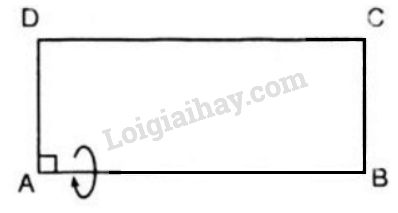
Diện tích hình chữ nhật \(ABCD\) là: \(AB.AD = 2a^2\)

Chu vi hình chữ nhật là: \(2(AB + CD) = 6a ⇒ AB + CD = 3a\)

Độ dài AB, CD có tổng là 3a, tích là \(2.a^2\) nên độ dài \(AB\) và \(CD\) là nghiệm của phương trình:

\({x^2}-{\rm{ }}3ax{\rm{ }}+{\rm{ }}2{a^2} = {\rm{ }}0\)

\(\begin{array}{l}
{x^2} - ax - 2ax + 2{a^2} = 0\\
\Leftrightarrow x\left( {x - a} \right) - 2a\left( {x - a} \right) = 0\\
\Leftrightarrow \left( {x - a} \right)\left( {x - 2a} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = a\\
x = 2a
\end{array} \right.
\end{array}\)

Vì \(AB > AD\) nên ta chọn \(AB = 2a; AD = a\)

Khi quay hình chữ nhật quanh \(AB\) ta được hình trụ có \(h=AB=2a\) và \(r=AD=a.\)

Vậy diện tích xung quanh hình trụ là:

\({S_{xq}} = 2\pi .AD.AB = 2\pi .a.2a = 4{\rm{ }}\pi {a^2}\)

Thể tích hình trụ là:

\(V{\rm{ }} = {\rm{ }}\pi {\rm{ }}.{\rm{ }}A{D^2}.{\rm{ }}AB{\rm{ }} = {\rm{ }}\pi .{\rm{ }}{a^2}.{\rm{ }}2a{\rm{ }} = {\rm{ }}2\pi {a^3}\)

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 6 phiếu

Bài tiếp theo

Bài 40 trang 129 SGK Toán 9 tập 2
Hãy tính diện tích toàn phần của các hình tương ứng theo các kích thước đã cho trên hình 115.
Bài 41 trang 129 SGK Toán 9 tập 2
a) Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi.
Bài 42 trang 130 SGK Toán 9 tập 2
Hãy tính thể tích các hình dưới đây theo kích thước đã cho (h.117).
Bài 43 trang 130 SGK Toán 9 tập 2
Hãy tính thể tích các hình dưới đây theo kích thước đã cho (h.118) (đơn vị : cm).
Bài 44 trang 130 SGK Toán 9 tập 2
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119).
Bài 45 trang 131 SGK Toán 9 tập 2
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.Hãy tính:
Lý thuyết Ôn tập chương 4. Hình trụ - Hình nón - Hình cầu
Lý thuyết Ôn tập chương 4. Hình trụ - Hình nón - Hình cầu
Bài 38 trang 129 SGK Toán 9 tập 2
Hãy tính thể tích , diện tích bề mặt một chi tiết máy theo kích thước đã cho trên hình 114.