-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 8 trang 80 SBT toán 8 tập 1
Giải bài 8 trang 80 sách bài tập toán 8. Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F...
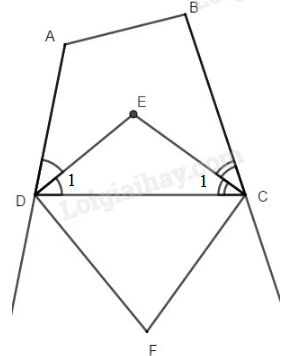
Đề bài
Tứ giác \(ABCD\) có \(\widehat A = {110^0},\)\(\widehat B = {100^0}.\) Các tia phân giác của các góc \(C\) và \(D\) cắt nhau ở \(E.\) Các đường phân giác của các góc ngoài tại các đỉnh \(C\) và \(D\) cắt nhau ở \(F.\) Tính \(\widehat {CED},\widehat {CFD}\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Tổng bốn góc của một tứ giác bằng \(360^o.\)
+) Hai tia phân giác của hai góc kề bù vuông góc với nhau.
Lời giải chi tiết
Vì DE là phân giác góc ADC nên \(\widehat {{D_1}} = \dfrac{1}{2}\widehat D\)
Vì CE là phân giác góc BCD nên \(\widehat {{C_1}} = \dfrac{1}{2}\widehat C\)
Trong tứ giác \(ABCD,\) ta có:
\( \widehat A + \widehat B + \widehat C + \widehat D = {360^0} \) (tổng 4 góc trong tứ giác)
\(\eqalign{
& \Rightarrow \widehat C + \widehat D = {360^0} - \left( {\widehat A + \widehat B} \right) \cr
& = {360^0} - \left( {{{110}^0} + {{100}^0}} \right) = {150^0} \cr
& {\widehat D_1} + {\widehat C_1} = {{\widehat C + \widehat D} \over 2} = {{{{150}^0}} \over 2} = {75^0} \cr} \)
Trong \(∆CED,\) ta có:
\(\widehat {CED} + {{{\widehat C}_1} + {{\widehat D}_1}} = {180^0} \) (tổng 3 góc trong tam giác)
\(\Rightarrow \widehat {CED} = {180^0} - \left( {{{\widehat C}_1} + {{\widehat D}_1}} \right) \)\(= {180^0} - {75^0} = {105^0}\)
Vì \(DE\) và \(DF\) là các tia phân giác của hai góc kề bù nên \(DE ⊥ DF\) (tính chất tia phân giác của hai góc kề bù)
\(\Rightarrow \widehat {EDF} = {90^0}\)
Vì \(CE\) và \(CF\) là các tia phân giác của hai góc kề bù nên \(CE ⊥ CF\) (tính chất tia phân giác của hai góc kề bù)
\( \Rightarrow \widehat {ECF} = {90^0}\)
Trong tứ giác \(CEDF,\) ta có:
\(\widehat {CED} + \widehat {EDF} + \widehat {CFD} + \widehat {ECF} = {360^0} \) (tổng 4 góc trong tứ giác)
\(\Rightarrow \widehat {CFD} = {360^0} - \left( {\widehat {CED} + \widehat {EDF} + \widehat {ECF}} \right)\)
\(\widehat {CFD} = {360^0} - \left( {{{105}^0} + {{90}^0} + {{90}^0}} \right)\)\(=360^0-285^0 = {75^0} \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9 trang 80 SBT toán 8 tập 1
- Bài 10 trang 80 SBT toán 8 tập 1
- Bài 1.1 phần bài tập bổ sung trang 81 SBT toán lớp 8 tập 1
- Bài 1.2 phần bài tập bổ sung trang 81 SBT toán lớp 8 tập 1
- Bài 1.3 phần bài tập bổ sung trang SBT toán lớp 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
