 Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
 Luyện tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong ta..
Luyện tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong ta..
Bài tập 35 trang 98 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC vuông tại A có đường phân giác BD. Kẻ DH vuông góc với BC tại H.
Đề bài
Cho tam giác ABC vuông tại A có đường phân giác BD. Kẻ DH vuông góc với BC tại H.
a) So sánh DA và DH
b) Chứng minh DA < DC.
c) Lấy điểm E trên tia đối của tia AC sao cho tam giác BED cân tại B. So sánh BE và BC.
Lời giải chi tiết
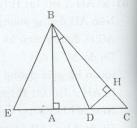
a) Xét ∆DAB vuông tại A và ∆DHB vuông tại H, ta có:
BD là cạnh chung
\(\widehat {ABD} = \widehat {DAH}\) (BD là tia phân giác của \(\widehat {ABC}\))
Do đó ∆DAB = ∆DHB (cạnh huyền – góc nhọn)
=> DA = DH.
b) \(DH \bot AC\) tại H, \(C \in AC \Rightarrow DH < DC\)
Mà DA = DH (câu a). Do đó DA < DC.
c) Ta có BE = BD (∆BED cân tại B)
Mà AD, AC lần lượt là hình chiếu của BD, BC trên AC và AD < AC
Nên BD < BC. Vậy BE < BC.
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận