-
CHƯƠNG 1. SỐ HỮU TỈ - SỐ THỰC
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC – ĐƯỜNG THẲNG SONG SONG
-
CHƯƠNG 2. TAM GIÁC
-
Chủ đề 3: Tam giác - Tam giác bằng nhau
- 1. Tổng ba góc trong một tam giác
- 2. Hai tam giác bằng nhau
- 3. Trường hợp bằng nhau thứ nhất của tam giác: Cạnh - cạnh - cạnh (c.c.c)
- 4. Trường hợp bằng nhau thứ hai của tam giác: Cạnh - góc - cạnh (c.g.c)
- 5. Trường hợp bằng nhau thứ ba của tam giác: Góc - góc - góc (g.g.g)
- Bài tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
- Luyện tập - Chủ đề 3: Tam giác - Tam giác bằng nhau
-
Chủ đề 4. Tam giác cân - Định lý Pythagore
-
Ôn tập chương 2 - Hình học 7
-
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4. BIỂU THỨC ĐẠI SỐ
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC – CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
-
Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- 1. Quan hệ giữa góc và cạnh trong một tam giác
- 2. Quan hệ giữa đường vuông góc và đường xiên – Giữa đường xiên và hình chiếu
- 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
- Luyện tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam giác
-
Chủ đề 6 : Các đường đồng quy của tam giác
- 1. Tính chất ba đường trung tuyến của tam giác
- 2. Tính chất tia phân giác của một góc
- 3. Tính chất ba đường phân giác của tam giác
- 4. Tính chất đường trung trực của một đoạn thẳng
- 5. Tính chất ba đường trung trực của tam giác
- 6. Tính chất ba đường cao trong tam giác
- Bài tập - Chủ đề 6 : Các đường đồng quy của tam giác
- Luyện tập - Chủ đề 6 : Các đường đồng quy của tam giác
-
Ôn tập chương 3 – Hình học
-
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
Bài tập - Chủ đề 5 : Quan hệ giữa các yếu tố trong tam ..
Bài tập 16 trang 97 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh với một điểm bất kì của cạnh đáy thì luôn luôn nhỏ hơn hoặc bằng độ dài cạnh bên.
Đề bài
Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh với một điểm bất kì của cạnh đáy thì luôn luôn nhỏ hơn hoặc bằng độ dài cạnh bên.
Lời giải chi tiết
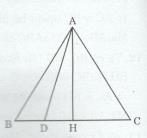
Xét ∆ABC cân tại A, D là điểm trên cạnh BC.
Cần chứng minh rằng AD ≤ AB
* Nếu \(D \equiv B\) thì AD = AB
* Nếu \(D \equiv C\) thì AD = AC = AB
* Nếu D khác B và C
Vẽ \(AH \bot BC\) tại H
* Nếu D thuộc đoạn thẳng HB (D khác B)
\(D \equiv H\) thì AD = AH < AB (đường vuông góc ngắn hơn mọi đường xiên).
\(D \ne H\) thì HD < HB, HD và HB lần lượt là hình chiếu của AD và AB trên BC
Do đó AD < AC.
* Nếu D thuộc đoạn thẳng HC
Tương tự trên có AD < AC = AB
Tóm lại AD ≤ AB.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 17 trang 97 Tài liệu dạy – học Toán 7 tập 2
- Bài tập 18 trang 97 Tài liệu dạy – học Toán 7 tập 2
- Bài tập 19 trang 97 Tài liệu dạy – học Toán 7 tập 2
- Bài tập 20 trang 97 Tài liệu dạy – học Toán 7 tập 2
- Bài tập 21 trang 97 Tài liệu dạy – học Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
