 Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7
 Ôn tập chương 3 – Hình học
Ôn tập chương 3 – Hình học
Bài tập 1 trang 127 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Ở hình 76, cho biết:
Đề bài
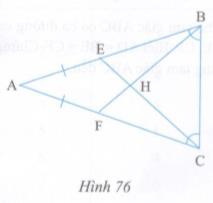
Ở hình 76, cho biết:
\(\eqalign{ & AE = AF \cr & \widehat {ABC} = \widehat {ACB} \cr}\)
Chứng minh AH là đường trung trực của BC.
Lời giải chi tiết
Ta có \(\widehat {ABC} = \widehat {ACB}\) (gt) => ∆ABC cân tại A => AB = AC
Mà AE = AF (gt). Nên AB – AE = AC – AF => BE = CF
Xét ∆BEC và ∆CFB ta có: BE = CF
\(\widehat {EBC} = \widehat {BCF}\) (gt)
BC (cạnh chung)
Do đó: ∆BEC = ∆CFB (c.g.c)
\( \Rightarrow \widehat {BCE} = \widehat {CBF} \Rightarrow \widehat {BCH} = \widehat {CBH}\) => ∆HBC cân tại H => HB = HC
Ta có: AB = AC (∆ABC cân tại A) và HB=HC
=> A và H cùng thuộc đường trung trực của BC.
Vậy AH là đường trung trực của BC.
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận