-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 8.2 phần bài tập bổ sung trang 93 SBT toán 8 tập 1
Giải bài 8.2 phần bài tập bổ sung trang 93 sách bài tập toán 8. Cho tam giác ABC, đường trung tuyến AM và trọng tâm G. Gọi I là điểm đối xứng với A qua G. Chứng minh rằng I là điểm đối xứng với G qua M.
Đề bài
Cho tam giác \(ABC,\) đường trung tuyến \(AM\) và trọng tâm \(G.\) Gọi \(I\) là điểm đối xứng với \(A\) qua \(G.\)
Chứng minh rằng \(I\) là điểm đối xứng với \(G\) qua \(M.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Ba đường trung tuyến trong tam giác cùng đi qua một điểm, điểm này cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến ứng với đỉnh đó.
+) Hai điểm gọi là đối xứng với nhau qua \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
Lời giải chi tiết
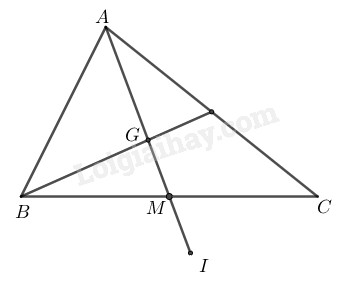
Tam giác ABC có G là trọng tâm và AM là đường trung tuyến nên \(A, G, M\) thẳng hàng.
Vì \(I\) đối xứng với \(A\) qua tâm \(G\) nên \(GA = GI\) và \(A, G, M, I\) thẳng hàng.
Lại có \(GM=\dfrac{1}{2} GA\) ( tính chất đường trung tuyến của tam giác)
Suy ra: \(GM=\dfrac{1}{2} GI\)
Mà: \(GM + MI = GI\)
Suy ra: \(GM = MI=\dfrac{1}{2} GI\) nên điểm \(M\) là trung điểm của \(GI\)
Vậy \(I\) đối xứng với \(G\) qua tâm \(M.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 8.1 phần bài tập bổ sung trang 93 SBT toán 8 tập 1
- Bài 105 trang 93 SBT toán 8 tập 1
- Bài 104 trang 93 SBT toán 8 tập 1
- Bài 103 trang 92 SBT toán 8 tập 1
- Bài 102 trang 92 SBT toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
