Bài 4.1, 4.2, 4.3 phần bài tập bổ sung trang 86 SBT toán 6 tập 2

Bài 4.1

Nhìn mỗi hình vẽ và điền đúng số đo góc vào ô còn trống trong bảng sau

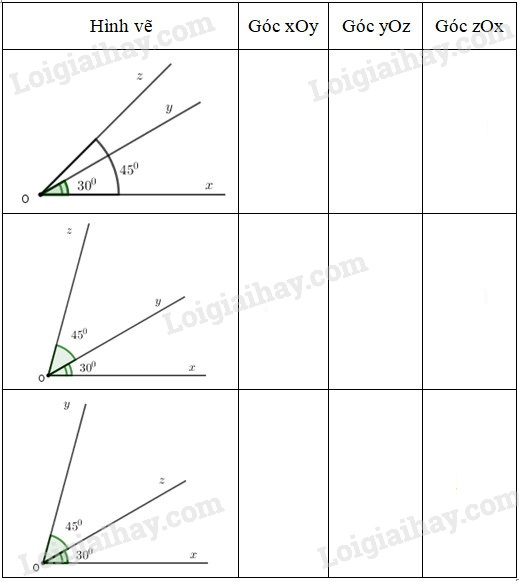
Phương pháp giải:

Áp dụng tính chất :

Nếu tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) thì \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\). 

Lời giải chi tiết:

•  Hình thứ nhất :

Vì tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) nên \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)

\(\Rightarrow \widehat{yOz}=\widehat{xOz} - \widehat{xOy} \)\(= 45^o - 30^o = 15^o.\)

•  Hình thứ hai :

Vì tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) nên \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)

\(\Rightarrow \widehat{xOz}=\widehat{xOy} + \widehat{yOz} \)\(= 30^o + 45^o = 75^o.\)

•  Hình thứ ba :

Vì tia \(Oz\) nằm giữa tia \(Ox\) và tia \(Oy\) nên \(\widehat{xOz}+\widehat{zOy}=\widehat{xOy}\)

\(\Rightarrow \widehat{xOy}=\widehat{xOz}+\widehat{zOy} \)\(= 30^o + 45^o = 75^o.\)

Vậy ta có bảng kết quả như sau :

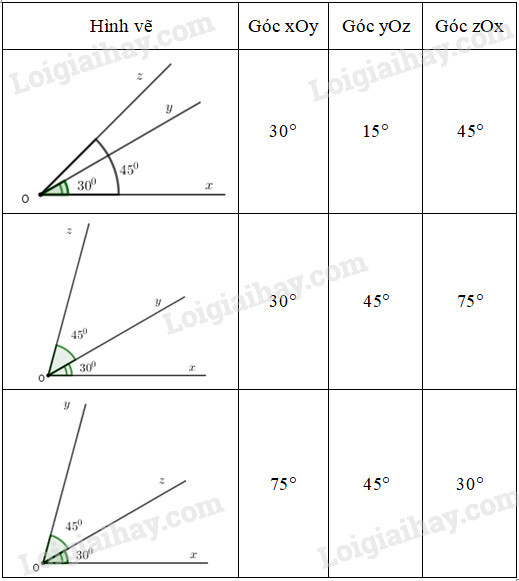
Bài 4.2

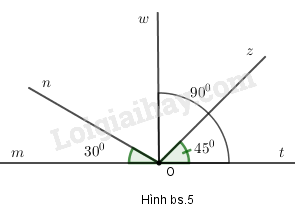
Cho hình bs.5

a) Gọi tên các cặp góc kề nhau đỉnh \(O\) trong hình đó.

b) Cho biết số đo của các góc đỉnh \(O\) trong hình đó.

c) Cho biết những cặp góc phụ nhau đỉnh \(O\).

d) Cho biết những cặp góc bù nhau đỉnh \(O\).

e) Cho biết những cặp góc kề bù nhau đỉnh \(O\). 

Phương pháp giải:

- Áp dụng định nghĩa :

+) Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh chung.

+) Hai góc phụ nhau là hai góc có tổng số đo bằng \(90^o\).

+) Hai góc bù nhau là hai góc có tổng số đo bằng \(180^o\) .

+) Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù.

- Áp dụng tính chất : Nếu tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) thì \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\). 

Lời giải chi tiết:

a) Các cặp góc kề nhau đỉnh \(O\) là: \(mOn\) và \(nOw\) ; \(mOn\) và \(nOz\) ; \(mOn\) và \(nOt\) ; \(mOw\) và \(zOw\) ; \(mOw\) và \(tOw\) ; \(mOz\) và \(zOt\) ; \(wOn\) và \(zOw\) ; \(wOn\) và \( tOw\) ; \( wOz\) và \(zOt\).

b) Quan sát hình vẽ ta thấy \(\widehat {mOw}\) và \(\widehat {wOt}\) là hai góc kề bù

\(\Rightarrow \widehat {mOw} + \widehat {wOt} =180^\circ\)

\(\Rightarrow \widehat {mOw}  =180^\circ - \widehat {wOt}\)

\(\Rightarrow \widehat {mOw}  =180^\circ - 90^\circ = 90^\circ\)

Lại có, trên cùng nửa mặt phẳng bờ là đường thẳng \(mt\) có \(\widehat {mOn} <\widehat {mOw}\) (do \(30^0<90^0)\) nên tia \(On\) nằm giữa tia \(Om\) và tia \(Ow.\) Do đó, \(\widehat{mOn}+\widehat{nOw}=\widehat{mOw}\)

\(\Rightarrow \widehat{nOw}=\widehat{mOw} - \widehat{mOn} \)\(=90^\circ - 30^\circ = 60^\circ \)

Trên cùng nửa mặt phẳng bờ là đường thẳng \(mt\) có \(\widehat {tOz} <\widehat {tOw}\) (do \(45^0<90^0)\) nên tia \(Oz\) nằm giữa tia \(Ot\) và tia \(Ow.\) Do đó, \(\widehat{tOz}+\widehat{zOw}=\widehat{tOw}\)

\(\Rightarrow \widehat{zOw}=\widehat{tOw} - \widehat{tOz} \)\(=90^\circ - 45^\circ = 45^\circ \)

Vậy : \(\widehat {mOt} = 180^\circ ;\widehat {mOw} = 90^\circ ;\)\(\widehat {now} = 60^\circ ;\widehat {{\rm{wO} }z} = 45^\circ \)

c) Các cặp góc phụ nhau đỉnh \(O\) là : \(mOn\) và \(nOw\) ; \(wOz\) và \( zOt\).

d) Các cặp góc bù nhau đỉnh \(O\) là : \(mOn\) và \(nOt\) ; \(wOm\) và \(wOt\) ; \(mOz\) và \(zOt\).

e) Các cặp góc kề bù nhau đỉnh \(O\) là : \(mOn\) và \(nOt\) ; \(wOm\) và \(wOt\) ; \(mOz\) và \(zOt\).

Bài 4.3

Mỗi câu sau đây là đúng hay sai ?

a) Ta luôn có \(\widehat {mOt} + \widehat {t{\rm{Ow}}} = \widehat {m{\rm{Ow}}}\); 

b) Nếu \(\widehat {mOt} + \widehat {t{\rm{Ow}}} = \widehat {m{\rm{Ow}}}\) thì tia Ot nằm giữa hai tia \(Om\) và \(Ow\);

c) Hai góc có tổng bằng \(180^\circ\) là hai góc kề bù;

d) Hai góc kề bù nếu tia đối của góc này là tia đối của góc kia;

e) Hai góc nhọn là hai góc phụ nhau;

f) Hai góc nhọn là hai góc bù nhau;

g) Hai góc vuông là hai góc kề bù;

h) Hai góc phụ nhau mà một góc là \(45^\circ\) thì góc kia là \(135^\circ\);

i) Hai góc bù nhau mà một góc là \(45^\circ\) thì góc kia là \(45\).

Phương pháp giải:

- Áp dụng định nghĩa :

+) Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh chung.

+) Hai góc phụ nhau là hai góc có tổng số đo bằng \(90^o\).

+) Hai góc bù nhau là hai góc có tổng số đo bằng \(180^o\) .

+) Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù.

- Áp dụng tính chất : Nếu tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) thì \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\). 

Lời giải chi tiết:

Trong bài này chỉ có câu b là đúng, các câu còn lại là sai. 

Giải thích:

a) Sai vì \(\widehat {mOt} + \widehat {t{\rm{Ow}}} = \widehat {m{\rm{Ow}}}\) chỉ đúng khi Ot là tia nằm giữa hai tia Om và Ow .

b) Đúng 

c) Sai vì hai góc có tổng bằng \(180°\) là hai góc bù nhau.

d) Sai vì hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.

e) Sai vì tổng số đo của hai góc nhọn có thể khác \(90°,\) ví dụ \(30^0+40^0=70^0 \ne 90^0\)

f) Sai vì tổng hai góc nhọn luôn nhỏ hơn \(180^0\)

g) Sai vì nếu hai góc vuông không có cạnh chung thì không phải là hai góc kề bù.

h) Sai vì hai góc phụ nhau là hai góc có tổng số đo bằng \(90°.\) Suy ra, biết số đo của một góc bằng \(45°\) thì số đo của góc còn lại cũng bằng \(90^0-45°=45^0.\)

i) Sai vì hai góc bù nhau là hai góc có tổng số đo bằng \(180°.\) Suy ra, biết số đo của một góc bằng \(45°\) thì số đo góc còn lại bằng \(180^0-45^0=135° .\) 

Loigiaihay.com