Bài 2.1, 2.2, 2.3, 2.4 phần bài tập bổ sung trang 7 SBT toán 6 tập 2
Giải bài 2.1, 2.2, 2.3, 2.4 phần bài tập bổ sung trang 7, 8 sách bài tập toán 6 tập 2. Hãy chọn câu trả lời đúng.
Bài 2.1
Phân số bằng phân số \(\displaystyle - {{16} \over {24}}\) là :
(A) \(\displaystyle{{16} \over {24}}\); (B) \(\displaystyle{{ - 2} \over { - 3}}\);
(C) \(\displaystyle{{ - 2} \over 3}\); (D) \(\displaystyle{{ - 16} \over { - 24}}\)
Hãy chọn đáp án đúng.
Phương pháp giải:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) được gọi là bằng nhau nếu \(a.d = b.c.\)
Lời giải chi tiết:
Trong các phân số đã cho, phân số bằng phân số \(\displaystyle - {{16} \over {24}}\) là \(\displaystyle{{ - 2} \over 3}\) vì tích chéo \((-16).3=24.(-2)\,(=-48)\)
Chọn đáp án (C)
Bài 2.2
Các cặp phân số bằng nhau là :
(A) \(\displaystyle{{ - 3} \over 4}\) và \(\displaystyle{{ - 4} \over 3}\); (B) \(\displaystyle - {2 \over 3}\) và \(\displaystyle{6 \over 9}\);
(C) \(\displaystyle{3 \over 7}\) và \(\displaystyle{{ - 3} \over 7}\); (D) \(\displaystyle{7 \over 8}\) và \(\displaystyle{{ - 35} \over { - 40}}\)
Hãy chọn câu trả lời đúng.
Phương pháp giải:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) được gọi là bằng nhau nếu \(a.d = b.c.\)
Lời giải chi tiết:
+) \(\displaystyle{{ - 3} \over 4}\ne \displaystyle{{ - 4} \over 3}\) vì \((-3). 3 \ne 4. (-4).\)
+) \(\displaystyle - {2 \over 3}\ne \displaystyle{6 \over 9}\) vì \((-2).9 \ne 3.6 .\)
+) \(\displaystyle{3 \over 7} \ne\displaystyle{{ - 3} \over 7}\) vì \( 3.7\ne 7.(-3)\)
+) \(\displaystyle{7 \over 8} = \displaystyle{{ - 35} \over { - 40}}\) vì \( 7.(-40) = 8. (-35)\,(=-280)\)
Chọn đáp án (D).
Bài 2.3
Hãy tìm các số nguyên \(x\) và \(y\), biết :
\(\displaystyle{{ - 2} \over x} = {y \over 3}\) và \(x < 0 < y.\)
Phương pháp giải:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) được gọi là bằng nhau nếu \(a.d = b.c.\)
Lời giải chi tiết:
Ta có \(\displaystyle{{ - 2} \over x} = {y \over 3}\)
\(\Rightarrow x.y = -2.3 = -6\) \(=(-1).6=(-3).2=(-6).1\)
Vì \(x < 0 < y\) nên ta có bảng sau :
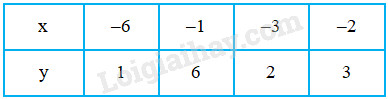
Bài 2.4
Tìm các số nguyên \(x\) và \(y\), biết :
\(\displaystyle{{x - 3} \over {y - 2}} = {3 \over 2}\) và \(x – y = 4\)
Phương pháp giải:
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) được gọi là bằng nhau nếu \(a.d = b.c.\)
Lời giải chi tiết:
\(\displaystyle{{x - 3} \over {y - 2}} = {3 \over 2}\) nên \(2(x \,– 3) = 3(y\, – 2)\)
\( \Rightarrow 2x – 6 = 3y – 6\) \(\Rightarrow 2x = 3y.\)
Theo đề bài ta có : \(x-y=4\)
\(\Rightarrow 2(x-y)=2.4\)
\(\Rightarrow 2x – 2y = 8\) mà \(2x=3y\)
\(\Rightarrow 3y-2y= 8\)
\(\Rightarrow y=8\)
Khi đó \(2.x=3.8\) \(\Rightarrow 2x=24 \Rightarrow x=24:2\)\(\Rightarrow x=12\)
Vậy \(\displaystyle y = 8\;;\;x = 12.\)
Loigiaihay.com













Danh sách bình luận