Giải bài tập, Sách bài tập (SBT) Toán 7 Bài 1. Tổng ba góc của một tam giác

Bài 2 trang 137 SBT toán 7 tập 1


Giải bài 2 trang 137 sách bài tập toán 7 tập 1. Cho tam giác ABC có góc A = 60^o ...

Đề bài

Cho tam giác ABC có \(\widehat A = 60^\circ ,\widehat C = 50^\circ \). Tia phân giác của góc B cắt AC ở D. Tính \(\widehat {ADB},\widehat {CDB}\).

Phương pháp giải - Xem chi tiết

Định lí: Tổng ba góc của một tam giác bằng \({180^0}\).

Lời giải chi tiết

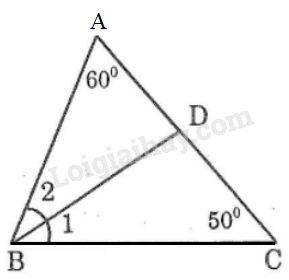
Áp dụng định lí tổng ba góc của một tam giác vào \(∆ABC\) ta có: 

\(\widehat A + \widehat B + \widehat C = 180^\circ \)

\(\eqalign{
& \Rightarrow \widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) \cr 
& \Rightarrow  \widehat B = 180^\circ - \left( {60^\circ + 50^\circ } \right) = 70^\circ \cr} \)

\(\displaystyle \widehat {{B_1}} = \widehat {{B_2}} = {1 \over 2}\widehat B\) (vì \(BD\) là tia phân giác góc \(B\))

\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = 70^\circ :2 = 35^\circ \)

Xét \(∆BDC\) ta có \(\widehat {A{\rm{D}}B}\) là góc ngoài tại đỉnh \(D\).

\( \Rightarrow \widehat {A{\rm{D}}B} = \widehat {{B_1}} + \widehat C\) (tính chất góc ngoài tam giác)

\( \Rightarrow \widehat {A{\rm{D}}B} = 35^\circ  + 50^\circ  = 85^\circ \)

\(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C} = 180^\circ \) (hai góc kề bù)

\( \Rightarrow \widehat {B{\rm{D}}C} = 180^\circ  - \widehat {A{\rm{D}}B} = 180^\circ  - 85^\circ  \)\(\,= 95^\circ \)

Loigiaihay.com


Bình chọn:
4.4 trên 30 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store