-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 16 trang 139 SBT toán 7 tập 1
Giải bài 16 trang 139 sách bài tập toán 7 tập 1. Cho tam giác ABC có góc A = 90^o, kẻ AH vuông góc với BC ...
Đề bài
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ \), kẻ \(AH\) vuông góc với \(BC\; (H ∈ BC).\) Các tia phân giác của các góc \(\widehat C\) và \(\widehat {BAH}\) cắt nhau ở \(I\). Chứng minh rằng: \(\widehat {AIC} = 90^\circ \)
Phương pháp giải - Xem chi tiết
- Định lí: Tổng ba góc của một tam giác bằng \({180^o}\)
- Trong tam giác vuông hai góc nhọn phụ nhau.
Lời giải chi tiết
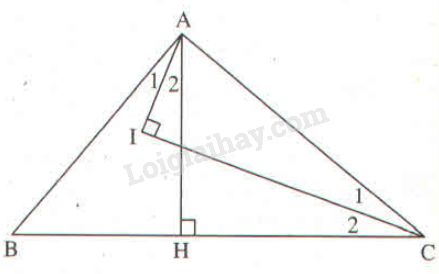
Ta có: \(AH \bot BC\left( {gt} \right) \Rightarrow \Delta AHB\) vuông tại \(H\).
Xét tam giác vuông \(AHB\) có \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow \widehat B + \widehat {BAH} = 90^\circ \left( 1 \right)\)
Xét tam giác vuông \(ABC\) có: \(\widehat {BAC} = 90^\circ \)
\( \Rightarrow \widehat B + \widehat C = 90^\circ \left( 2 \right)\)
Từ (1) và (2) suy ra: \(\widehat {BAH} = \widehat C\)
+) Vì AI là tia phân giác của góc BAH nên:
\( \widehat {{A_1}} = \widehat {{A_2}} = {1 \over 2}\widehat {BAH}\left( {gt} \right) \)
+) Vì CI là tia phân giác của góc ACB nên:
\( \widehat {{C_1}} = \widehat {{C_2}} = {1 \over 2}\widehat C\left( {gt} \right) \)
Mà \(\widehat {BAH} = \widehat C\) suy ra \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
Lại có \(\widehat {{A_1}} + \widehat {IAC} = \widehat {BAC} = 90^\circ \)
Suy ra: \(\widehat {{C_1}} + \widehat {IAC} = 90^\circ \)
Áp dụng định lí tổng các góc của một tam giác vào \(∆ AIC\), ta có:
\(\widehat {AIC} + \widehat {IAC} + \widehat {{C_1}} = {180^o}\)
\( \Rightarrow \widehat {AIC} = {180^o} - \left( {\widehat {IAC} + \widehat {{C_1}}} \right) \)\(\,= {180^o} - {90^o}= 90^\circ \).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 17 trang 139 SBT toán 7 tập 1
- Bài 18 trang 139 SBT toán 7 tập 1
- Bài 1.1, 1.2, 1.3, 1.4 phần bài tập bổ sung trang 139 SBT toán 7 tập 1
- Bài 15 trang 138 SBT toán 7 tập 1
- Bài 14 trang 138 SBT toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
