Giải bài tập, Sách bài tập (SBT) Toán 7 Bài 1. Tổng ba góc của một tam giác

Bài 1.1, 1.2, 1.3, 1.4 phần bài tập bổ sung trang 139 SBT toán 7 tập 1


Giải bài 1.1, 1.2, 1.3, 1.4 phần bài tập bổ sung trang 139 sách bài tập toán 7 tập 1. Tam giác ABC có góc A = 40^o. Các tia phân giác góc B và C cắt nhau tại I ...

Lựa chọn câu để xem lời giải nhanh hơn

Bài 1.1

Tam giác \(ABC\) có \(\widehat A = {40^o}\). Các tia phân giác của các góc \(B\) và \(C\) cắt nhau ở \(I.\)

Góc \(BIC\) bằng:

(A) \(40^o\);

(B) \(70^o\);

(C) \(110^o\);

(D) \(140^o\). 

Phương pháp giải:

Định lí: Tổng ba góc của một tam giác bằng \({180^0}\).

Lời giải chi tiết:

 

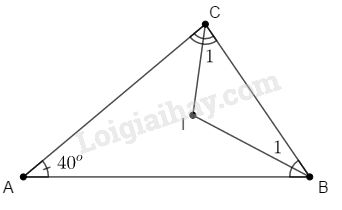
Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\) ta có:

\(\begin{array}{l}
\widehat A + \widehat B + \widehat C = {180^o}\\
\Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\\
\Rightarrow \widehat B + \widehat C = {180^o} - {40^o} = {140^o}
\end{array}\)

\(\widehat {{B_1}} = \dfrac{1}{2}\widehat B\) (vì \(BI\) là tia phân giác góc \(B\)).

\(\widehat {{C_1}} = \dfrac{1}{2}\widehat C\) (vì \(CI\) là tia phân giác góc \(C\)).

\( \Rightarrow \widehat {{B_1}} + \widehat {{C_1}}\)\( = \dfrac{1}{2}\left( {\widehat B + \widehat C} \right)\)

Áp dụng định lí tổng các góc của một tam giác vào \(\Delta BIC\) ta có: 

\(\begin{array}{l}
\widehat {{B_1}} + \widehat {{C_1}} + \widehat {BIC} = {180^o}\\
\Rightarrow \widehat {BIC} = {180^o} - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right)\\
\Rightarrow \widehat {BIC} = {180^o} - \dfrac{1}{2}\left( {\widehat B + \widehat C} \right)\\
\Rightarrow \widehat {BIC} = {180^o} - \dfrac{1}{2}{.140^o} = {110^o}
\end{array}\)

Chọn C.

Bài 1.2

Tam giác \(ABC\) có \(\widehat A = {75^o}\). Tính \(\widehat B\) và \(\widehat C\), biết :

a) \(\widehat B = 2\widehat C\);

b) \(\widehat B - \widehat C = {25^o}\). 

Phương pháp giải:

Định lí: Tổng ba góc của một tam giác bằng \({180^0}\).

Lời giải chi tiết:

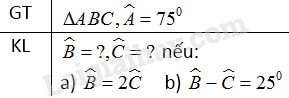
Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\), ta có:

\(\begin{array}{l}
\widehat A + \widehat B + \widehat C = {180^o}\\
\Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\\
\Rightarrow \widehat B + \widehat C = {180^o} - {75^o} = {105^o}\,\,\,\,(1)
\end{array}\)

a) Thay \(\widehat B = 2\widehat C\) vào (1) ta được:

\(\begin{array}{l}
2\widehat C + \widehat C = {105^o}\\
\Rightarrow 3\widehat C = {105^o}\\
\Rightarrow \widehat C = {105^o}:3 = {35^o}\\
\Rightarrow \widehat B = 2\widehat C = {2.35^o} = {70^o}
\end{array}\)

b) \(\widehat B - \widehat C = {25^o} \Rightarrow \widehat B = \widehat C + {25^o}\,\,\,(2)\)

Thay (2) vào (1) ta được:

\(\begin{array}{l}
\widehat C + {25^o} + \widehat C = {105^o}\\
\Rightarrow 2\widehat C + {25^o} = {105^o}\\
\Rightarrow 2\widehat C = {105^o} - {25^o}\\
\Rightarrow 2\widehat C = {80^o}\\
\Rightarrow \widehat C = {80^o}:2 = {40^o}\\
\Rightarrow \widehat B = \widehat C + {25^o} = {40^o} + {25^o} = {65^o}
\end{array}\) 

Bài 1.3

Tam giác \(ABC\) có \(\widehat B = {110^o},\widehat C = {30^o}\). Gọi \(Ax\) là tia đối của tia \(AC.\) Tia phân giác của góc \(BAx\) cắt đường thẳng \(BC\) tại \(K.\) Chứng minh rằng tam giác \(KAB\) có hai góc bằng nhau. 

Phương pháp giải:

- Góc ngoài tam giác bằng tổng hai góc trong không kề với nó.

- Tổng số đo hai góc kề bù bằng \(180^o\).

Lời giải chi tiết:

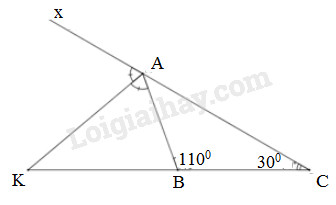
+ Ta có \(\widehat {ABK}\) và \(\widehat {ABC}\) là hai góc kề bù nên \(\widehat {ABK}+\widehat {ABC}=180^0\)

\(\Rightarrow \widehat {ABK} =180^0-\widehat {ABC}\)\(= {180^o} - {110^o} = {70^o}\)   (1)

+ Xét tam giác ACB có \(\widehat {BAx}\) là góc ngoài tại đỉnh A  nên: 

\(\widehat {BAx} = {110^o} + {30^o} = {140^o}\) (tính chất góc ngoài tam giác)

+ Do đó: 

\(\widehat {BAK} = \dfrac{1}{2}\widehat {BAx} = \dfrac{1}{2}{.140^o} = {70^o}\) (vì \(AK\) là tia phân giác góc \(A\))   (2) 

Từ (1) và (2) suy ra tam giác \(KAB\) có hai góc bằng nhau.

Bài 1.4

Cho tam giác \(ABC\) vuông tại \(A.\) Gọi \(d\) là đường thẳng vuông góc với \(BC\) tại \(C.\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D\) và cắt \(d\) ở \(E.\) Chứng minh rằng tam giác \(CDE\) có hai góc bằng nhau. 

Phương pháp giải:

- Trong tam giác vuông hai góc nhọn phụ nhau.

- Hai góc đối đỉnh thì bằng nhau.

Lời giải chi tiết:

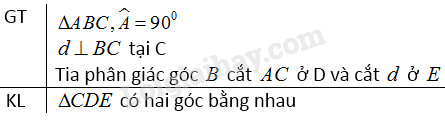
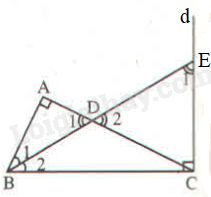
+) Ta có: \(\widehat {{D_1}} = \widehat {{D_2}}\) (hai góc đối đỉnh).

+) Tam giác ABD vuông tại A nên: 

\(\widehat {{D_1}} + \widehat {{B_1}} = {90^o}\) (trong tam giác vuông hai góc nhọn phụ nhau).

\( \Rightarrow \widehat {{D_2}} + \widehat {{B_1}} = {90^o}\)      (*)

+) Tam giác BCE vuông tại C nên: 

\(\widehat {{B_2}} + \widehat {{E_1}} = {90^o}\) (trong tam giác vuông hai góc nhọn phụ nhau).

Mặt khác \(\widehat {{B_1}} = \widehat {{B_2}}\) (vì \(BE\) là phân giác góc \(B\)).

\( \Rightarrow \widehat {{B_1}} + \widehat {{E_1}} = {90^o}\)      (2*)

Từ (*) và (2*) suy ra: \(\widehat {{D_2}} = \widehat {{E_1}}\).
 
Vậy tam giác \(CDE\) có hai góc bằng nhau.

Loigiaihay.com


Bình chọn:
4.2 trên 10 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store