Giải SBT đại số, hình học toán lớp 6 tập 1, tập 2 Ôn tập chương 2 - Số nguyên

Bài 159 trang 93 SBT toán 6 tập 1


Giải bài 159 trang 93 sách bài tập toán 6. Trên trục số cho hai điểm c, d (hình 28). a) Xác định các điểm - c, - d trên trục số ...

Đề bài

Trên trục số cho hai điểm \(c, d\) (hình \(28\)).

 

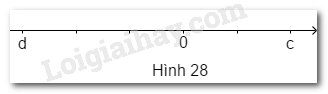
\(a)\) Xác định các điểm \(- c, - d\) trên trục số.

\(b)\) Xác định các điểm \(\left| c \right|,\left| d \right|,\left| { - c} \right|,\left| { - d} \right|\) trên trục số

\(c)\) So sánh các điểm \(c, d, -c, -d,\) \(\left| c \right|,\left| d \right|,\left| { - c} \right|,\left| { - d} \right|\) với \(0\)

Phương pháp giải - Xem chi tiết

Sử dụng:

+) Trên trục số: Số nằm bên phải số \(0\) là một số dương và số nằm bên trái số \(0\) là một số âm

+) \(a\) và \(-a\) là hai số đối nhau (tức cùng cách điểm \(0\) một khoảng bằng nhau nhưng nằm về hai phía của điểm \(0\))

+) Áp dụng \(|x|=a\) thì \(x=a\) khi \(x\) \( \ge \) \(0\) hoặc \(x=-a\) khi \(x<0.\) 

Lời giải chi tiết

\(a), b)\) Các điểm \(-c, -d,\) \(\left| c \right|,\) \(\left| d \right|,\) \(\left| { - c} \right|,\) \(\left| { - d} \right|\) được biểu diễn trên trục số.

 

\(c)\) Vì \(c > 0\) nên \(-c{\rm{ }} < {\rm{ }}0{\rm{ }},\,\left| c \right| > 0,\,\left| { - c} \right| > 0\)

 Vì \(d < 0\) nên \(- d > 0,\,\left| d \right| > 0,\,\left| { - d} \right| > 0\)

Loigiaihay.com


Bình chọn:
4.5 trên 14 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua