-
PHẦN SỐ HỌC - SBT TOÁN 6 TẬP 1
-
CHƯƠNG 1: ÔN TẬP VẢ BỔ TÚC VỀ SỐ TỰ NHIÊN
- Bài 1. Tập hợp. Phần tử của tập hợp
- Bài 2. Tập hợp các số tự nhiên
- Bài 3. Ghi số tự nhiên
- Bài 4. Số phần tử của một tập hợp. Tập hợp con
- Bài 5. Phép cộng và phép nhân
- Bài 6. Phép trừ và phép chia
- Bài 7. Luỹ thừa với số mũ tự nhiên, nhân hai luỹ thừa cùng cơ số
- Bài 8. Chia hai luỹ thừa cũng cơ số
- Bài 9. Thứ tự thực hiện các phép tính
- Bài 10. Tính chất chia hết của một tổng
- Bài 11. Dấu hiệu chia hết cho 2, cho 5
- Bài 12. Dấu hiệu chia hết cho 3, cho 9
- Bài 13. Ước và bội
- Bài 14. Số nguyên tố, hợp số. Bảng nguyên tố
- Bài 15. Phân tích một số ra thừa số nguyên tố
- Bài 16. Ước chung và bội chung
- Bài 17. Ước chung lớn nhất
- Bài 18. Bội chung nhỏ nhất
- Ôn tập chương 1 - Ôn tập và bổ túc về số tự nhiên
-
CHƯƠNG 2: SỐ NGUYÊN
- Bài 1. Làm quen với số nguyên âm
- Bài 2. Tập hợp các số nguyên
- Bài 3. Thứ tự trong tập hợp các số nguyên
- Bài 4. Cộng hai số nguyên cùng dấu
- Bài 5. Cộng hai số nguyên khác dấu
- Bài 6. Tính chất của phép cộng các số nguyên
- Bài 7. Phép trừ hai số nguyên
- Bài 8. Quy tắc dấu ngoặc
- Bài 9. Quy tắc chuyển vế
- Bài 10. Nhân hai số nguyên khác dấu
- Bài 11. Nhân hai số nguyên cùng dấu
- Bài 12. Tính chất của phép nhân
- Bài 13. Bội và ước của một số nguyên
- Ôn tập chương 2 - Số nguyên
-
-
PHẦN HÌNH HỌC - SBT TOÁN 6 TẬP 1
-
CHƯƠNG 1: ĐOẠN THẲNG
- Bài 1. Điểm. Đường thẳng
- Bài 2. Ba điểm thẳng hàng
- Bài 3. Đường thẳng đi qua hai điểm
- Bài 4. Thực hành trồng cây thẳng hàng
- Bài 5. Tia
- Bài 6. Đoạn thẳng
- Bài 7. Độ dài đoạn thẳng
- Bài 8. Khi nào thì AM + MB = AB?
- Bài 9. Vẽ đoạn thẳng cho biết độ dài
- Bài 10. Trung điểm của đoạn thẳng
- Ôn tập chương 1 - Đoạn thẳng
-
-
PHẦN SỐ HỌC - SBT TOÁN 6 TẬP 2
-
CHƯƠNG 3: PHÂN SỐ
- Bài 1. Mở rộng khái niệm phân số
- Bài 2. Phân số bằng nhau
- Bài 3. Tính chất cơ bản của phân số
- Bài 4. Rút gọn phân số
- Bài 5. Quy đồng mẫu nhiều phân số
- Bài 6. So sánh phân số
- Bài 7. Phép cộng phân số
- Bài 8. Tính chất cơ bản của phép cộng phân số
- Bài 9. Phép trừ phân số
- Bài 10. Phép nhân phân số
- Bài 11. Tính chất cơ bản của phép nhân phân số
- Bài 12. Phép chia phân số
- Bài 13. Hỗn số. Số thập phân. Phần trăm
- Bài 14. Tìm giá trị phân số của một số cho trước
- Bài 15. Tìm một số biết giá trị một phân số của nó
- Bài 16. Tìm tỉ số của hai số
- Bài 17. Biểu đồ phần trăm
- Bài tập ôn tập chương 3 - Phân số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 6 TẬP 2
Bài 152 trang 91 SBT toán 6 tập 1
Giải bài 152 trang 91 sách bài tập toán 6. Cho hai tập hợp số A và B: a) Có thể lập được bao nhiêu tổng dạng (a+b) với a ∈ A, b ∈ B?
Đề bài
Cho hai tập hợp số \({\rm{A}} = \left\{ {4;\,5;\,6;\,7;\,8} \right\};B = \left\{ {13;\,14;\,15} \right\}\)
\(a)\) Có thể lập được bao nhiêu tổng dạng \((a+b)\) với \(a ∈ A, b ∈ B\)\(?\)
\(b)\) Trong các tổng trên có bao nhiêu tổng chia hết cho \(3\)\(?\)
Phương pháp giải - Xem chi tiết
\(a)\) Lấy mỗi phần tử \(a ∈ A\) cộng với một phần tử \(b ∈ B\) ta được một tổng \(a+b\)
\(b)\) Sau khi tính tổng xong, xét xem có bao nhiêu tổng chia hết cho \(3\).
Lời giải chi tiết
\(a)\) Các giá trị của \(a,\, b\) và \(a+b\) được thể hiện trong bảng dưới đây, có \(15\) tổng với \(7\) giá trị khác nhau được tạo thành:
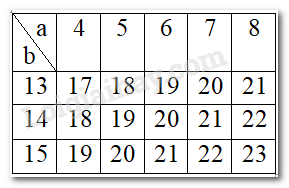
\(b)\) Trong đó, có \(5\) tổng chia hết cho \(3\) là: \(18, \,18,\, 21,\,21,\,21.\)
Như vậy có \(2\) tổng khác nhau chia hết cho \(3\) là: \(18\) và \(21\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 153 trang 91 SBT toán 6 tập 1
- Bài 154 trang 91 SBT toán 6 tập 1
- Bài 155 trang 91 SBT toán 6 tập 1
- Bài 156 trang 91 SBT toán 6 tập 1
- Bài 157 trang 91 SBT toán 6 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
