-
PHẦN SỐ HỌC - SBT TOÁN 6 TẬP 1
-
CHƯƠNG 1: ÔN TẬP VẢ BỔ TÚC VỀ SỐ TỰ NHIÊN
- Bài 1. Tập hợp. Phần tử của tập hợp
- Bài 2. Tập hợp các số tự nhiên
- Bài 3. Ghi số tự nhiên
- Bài 4. Số phần tử của một tập hợp. Tập hợp con
- Bài 5. Phép cộng và phép nhân
- Bài 6. Phép trừ và phép chia
- Bài 7. Luỹ thừa với số mũ tự nhiên, nhân hai luỹ thừa cùng cơ số
- Bài 8. Chia hai luỹ thừa cũng cơ số
- Bài 9. Thứ tự thực hiện các phép tính
- Bài 10. Tính chất chia hết của một tổng
- Bài 11. Dấu hiệu chia hết cho 2, cho 5
- Bài 12. Dấu hiệu chia hết cho 3, cho 9
- Bài 13. Ước và bội
- Bài 14. Số nguyên tố, hợp số. Bảng nguyên tố
- Bài 15. Phân tích một số ra thừa số nguyên tố
- Bài 16. Ước chung và bội chung
- Bài 17. Ước chung lớn nhất
- Bài 18. Bội chung nhỏ nhất
- Ôn tập chương 1 - Ôn tập và bổ túc về số tự nhiên
-
CHƯƠNG 2: SỐ NGUYÊN
- Bài 1. Làm quen với số nguyên âm
- Bài 2. Tập hợp các số nguyên
- Bài 3. Thứ tự trong tập hợp các số nguyên
- Bài 4. Cộng hai số nguyên cùng dấu
- Bài 5. Cộng hai số nguyên khác dấu
- Bài 6. Tính chất của phép cộng các số nguyên
- Bài 7. Phép trừ hai số nguyên
- Bài 8. Quy tắc dấu ngoặc
- Bài 9. Quy tắc chuyển vế
- Bài 10. Nhân hai số nguyên khác dấu
- Bài 11. Nhân hai số nguyên cùng dấu
- Bài 12. Tính chất của phép nhân
- Bài 13. Bội và ước của một số nguyên
- Ôn tập chương 2 - Số nguyên
-
-
PHẦN HÌNH HỌC - SBT TOÁN 6 TẬP 1
-
CHƯƠNG 1: ĐOẠN THẲNG
- Bài 1. Điểm. Đường thẳng
- Bài 2. Ba điểm thẳng hàng
- Bài 3. Đường thẳng đi qua hai điểm
- Bài 4. Thực hành trồng cây thẳng hàng
- Bài 5. Tia
- Bài 6. Đoạn thẳng
- Bài 7. Độ dài đoạn thẳng
- Bài 8. Khi nào thì AM + MB = AB?
- Bài 9. Vẽ đoạn thẳng cho biết độ dài
- Bài 10. Trung điểm của đoạn thẳng
- Ôn tập chương 1 - Đoạn thẳng
-
-
PHẦN SỐ HỌC - SBT TOÁN 6 TẬP 2
-
CHƯƠNG 3: PHÂN SỐ
- Bài 1. Mở rộng khái niệm phân số
- Bài 2. Phân số bằng nhau
- Bài 3. Tính chất cơ bản của phân số
- Bài 4. Rút gọn phân số
- Bài 5. Quy đồng mẫu nhiều phân số
- Bài 6. So sánh phân số
- Bài 7. Phép cộng phân số
- Bài 8. Tính chất cơ bản của phép cộng phân số
- Bài 9. Phép trừ phân số
- Bài 10. Phép nhân phân số
- Bài 11. Tính chất cơ bản của phép nhân phân số
- Bài 12. Phép chia phân số
- Bài 13. Hỗn số. Số thập phân. Phần trăm
- Bài 14. Tìm giá trị phân số của một số cho trước
- Bài 15. Tìm một số biết giá trị một phân số của nó
- Bài 16. Tìm tỉ số của hai số
- Bài 17. Biểu đồ phần trăm
- Bài tập ôn tập chương 3 - Phân số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 6 TẬP 2
Bài 3.2 phần bài tập bổ sung trang 126 SBT toán 6 tập 1
Giải bài 3.2 phần bài tập bổ sung trang 126 sách bài tập toán 6. Vẽ từng hình theo mỗi cách diễn đạt sau đây.a) Hai đường thẳng có chỉ một điểm chung...
Đề bài
Vẽ từng hình theo mỗi cách diễn đạt sau đây
a) Hai đường thẳng có chỉ một điểm chung.
b) Hai đường thẳng có đúng hai điểm chung.
c) Hai đường thẳng có đúng ba điểm chung.
d) Hai đường thẳng không song song với nhau.
Phương pháp giải - Xem chi tiết
- Hai đường thẳng không có điểm chung nào được gọi là hai đường thẳng song song.
- Hai đường thẳng chỉ có một điểm chung được gọi là hai đường thẳng cắt nhau.
Điểm chung của hai dường thẳng gọi là giao điểm của hai đường thẳng đó.
- Hai đường thẳng có vô số điểm chung gọi là hai đường thẳng trùng nhau.
Lời giải chi tiết
a)
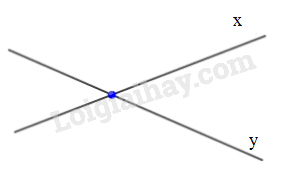
b) c) Hai đường thẳng có 2 hoặc 3 điểm chung là hai đường thẳng trùng nhau
d) Hai đường thẳng cắt nhau hoặc trùng với nhau.
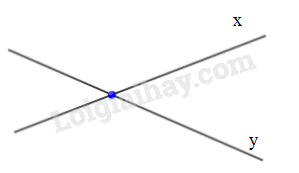
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3.3 phần bài tập bổ sung trang 126 SBT toán 6 tập 1
- Bài 3.1 phần bài tập bổ sung trang 126 SBT toán 6 tập 1
- Bài 22 trang 125 SBT toán 6 tập 1
- Bài 21 trang 125 SBT toán 6 tập 1
- Bài 20 trang 125 SBT toán 6 tập 1
>> Xem thêm
Tham Gia Group Dành Cho Lớp 6 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
