 Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học
 CHƯƠNG IV. HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU
CHƯƠNG IV. HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU
Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 4 - Hình học 9
Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 4 - Hình học 9
Đề bài
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD sao cho CD //AB và \(CD = R\sqrt 3 \).
a) Tính diện tích hình thang ABDC.
b) Tính thể tích của hình được sinh ra khi quay hình thang ABDC quanh AB.
Phương pháp giải - Xem chi tiết
Công thức tính diện tích hình thang: \(S = \frac{{\left( {a + b} \right).h}}{2}\)
Công thức tính thể tích hình nón : \({V_n} = {1 \over 3}\pi {R^2}h \)
Công thức tính thể tích hình trụ: \({V_t} = \pi {R^2}h\)
(Thể tích của hình sinh ra là :\(V = {V_t} + 2{V_n}\))
Lời giải chi tiết
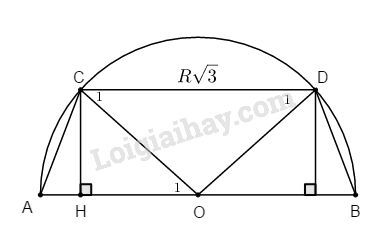
a) Ta có : \(CD = R\sqrt 3 \left( {gt} \right) \Rightarrow \widehat {COD} = 120^\circ \)
∆COD cân tại O \( \Rightarrow \widehat {{C_1}} = \widehat {{D_1}} = 30^\circ \)
CD // AB (gt) \( \Rightarrow \widehat {{O_1}} = \widehat {{C_1}} = 30^\circ \) (so le trong)
Kẻ CH vuông góc với AB tại H, ta có ∆CHO vuông, có \(\widehat {{O_1}} = 30^\circ \) nên \(CH = CO.\sin 30^\circ = {R \over 2}\)
Vậy \({S_{ABDC}} = {{\left( {AB + CD} \right).CH} \over 2} = {{\left( {2R + R\sqrt 3 } \right).{R \over 2}} \over 2} \)\(\;= {{{R^2}\left( {2 + \sqrt 3 } \right)} \over 4}\).
b) Khi quay hình thang ABDC quanh cạnh đáy AB ta được hình sinh ra gồm một hình trụ có bán kính đáy là \(CH = {R \over 2}\), chiều cao \(CD = R\sqrt 3 \) và hai hình nón bằng nhau có bán kính đáy là \(CH = {R \over 2}\) và chiều cao AH.
Trong tam giác vuông CHO, ta có :
\(HO = \sqrt {C{O^2} - C{H^2}} = \sqrt {{R^2} - {{\left( {{R \over 2}} \right)}^2}} \)\(\;= {{R\sqrt 3 } \over 2}\)
\( \Rightarrow AH = AO - HO = R - {{R\sqrt 3 } \over 2} \)\(\;= {{R\left( {2 - \sqrt 3 } \right)} \over 2}\)
Vậy ta gọi Vn là thể tích hình nón.
\({V_n} = {1 \over 3}\pi {R^2}h = {1 \over 3}\pi .C{H^2}.AH\)\(\; = {1 \over 3}\pi {\left( {{R \over 2}} \right)^2}.{{R\left( {2 - \sqrt 3 } \right)} \over 2} = {{\pi {R^3}\left( {2 - \sqrt 3 } \right)} \over {24}}\)
Do đó hai hình tròn bằng nhau có thể tích là : \(2{V_n} = {{\pi {R^3}\left( {2 - \sqrt 3 } \right)} \over {12}}\)
Và gọi Vt là thể tích hình trụ :
\({V_t} = \pi {R^2}h = \pi .C{H^2}.CD \)\(\;= \pi {\left( {{R \over 2}} \right)^2}.R\sqrt 3 = {{\pi {R^3}\sqrt 3 } \over 4}\)
Vậy thể tích của hình sinh ra là :
\(V = {V_t} + 2{V_n} = {{\pi {R^3}\sqrt 3 } \over 4} + {{\pi {R^3}\left( {2 - \sqrt 3 } \right)} \over {12}}\)
\(\;\;\;\; = {{3\pi {R^3}\sqrt 3 + 2\pi {R^3} - \pi {R^3}\sqrt 3 } \over {12}} = {{2\pi {R^3}\sqrt 3 + 2\pi {R^3}} \over {12}} \)
\(\;\;\;\;= {{\pi {R^3}\left( {\sqrt 3 + 1} \right)} \over 6}\).
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận