Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7 Luyện tập - Chủ đề 1: Góc tạo bởi các đường thẳng

Bài tập 4 trang 118 Tài liệu dạy – học Toán 7 tập 1


Đề bài

Cho hai đường thẳng cắt nhau tạo thành bốn góc \({O_1};\,\,{O_2};\,\,{O_3};\,\,{O_4}\) . Tính các góc còn lại trong các trường hợp sau:

a) \(\widehat {{O_1}} = {75^o}\)

b) \(\widehat {{O_1}} + \widehat {{O_3}} = {140^o}\)

c) \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = {240^o}\)

d) \(\widehat {{O_2}} - \widehat {{O_1}} = {30^o}\)

e) \(\widehat {{O_2}} = 2\widehat {{O_1}}\)

Lời giải chi tiết

 

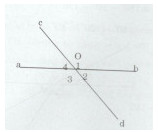
a)Ta có:

\(\widehat {{O_3}} = \widehat {{O_2}} = {75^0}\)  (hai góc đối đỉnh)

\(\widehat {{O_1}} + \widehat {{O_2}} = {180^0}\)  (hai góc kề bù)

\( \Rightarrow \widehat {{O_2}} = {180^0} - {75^0} = {105^0}\)

\(\widehat {{O_4}} = \widehat {{O_2}} = {105^0}\)  (hai góc đối đỉnh)

b) Ta có: \(\widehat {{O_1}} + \widehat {{O_3}} = {140^0}\)  mà \(\widehat {{O_1}} = \widehat {{O_3}}\)  (hai góc đối đỉnh)

Nên \(\widehat {{O_1}} + \widehat {{O_1}} = {140^0} \Rightarrow 2\widehat {{O_1}} = {140^0} \Rightarrow \widehat {{O_1}} = {{{{140}^0}} \over 2} = {70^0}\)

Do đó: \(\widehat {{O_3}} = \widehat {{O_1}} = {70^0}\)

\(\widehat {{O_1}} + \widehat {{O_2}} = {180^0}\)  (hai góc kề bù)

\( \Rightarrow \widehat {{O_2}} = {180^0} - {70^0} = {110^0}\)

\(\widehat {{O_4}} = \widehat {{O_2}} = {110^0}\)  (hai góc đối đỉnh)

c) Ta có: *\(\widehat {{O_1}} + \widehat {{O_2}} = {180^0}\)  (hai góc kề bù) mà \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = {240^0}\)  (giả thiết)

Nên \(\widehat {{O_3}} = {240^0} - {180^0} = {60^0}\)

*\(\widehat {{O_1}} = \widehat {{O_3}} = {60^0}\)  (hai góc đối đỉnh)

*\(\widehat {{O_1}} + \widehat {{O_2}} = {180^0}\)  (hai góc kề bù)

\( \Rightarrow \widehat {{O_2}} = {180^0} - {60^0} = {120^0}\)

\(\widehat {{O_4}} = \widehat {{O_2}} = {120^0}\)  (hai góc đối đỉnh)

d) Ta có: * \(\widehat {{O_2}} - \widehat {{O_1}} = {30^0}\) (giả thiết)

\( \Rightarrow \widehat {{O_2}} = {30^0} + \widehat {{O_1}}\)

Ta có: * \(\widehat {{O_1}} + \widehat {{O_2}} = {180^0}\)  (hai góc kề bù)

\(\eqalign{  &  \Rightarrow \widehat {{O_1}} + {30^0} + \widehat {{O_1}} = {180^0} \Rightarrow 2\widehat {{O_1}} = {150^0}  \cr  &  \Rightarrow \widehat {{O_1}} = {{{{150}^0}} \over 2} = {75^0} \cr} \)

*\(\widehat {{O_3}} = \widehat {{O_1}} = {75^0}\)  (hai góc đối đỉnh)

*\(\widehat {{O_2}} = {30^0} + \widehat {{O_1}} = {30^0} + {75^0} = {105^0}\)

*\(\widehat {{O_4}} = \widehat {{O_2}} = {105^0}\)  (hai góc đối đỉnh)

e) Ta có: \(\widehat {{O_2}} + \widehat {{O_1}} = {180^0}\)  (hai góc kề bù) mà \(\widehat {{O_2}} = 2\widehat {{O_1}}\)  (giả thiết)

\(\eqalign{  &  \Rightarrow 2\widehat {{O_1}} + \widehat {{O_1}} = {180^0}  \cr  &  \Rightarrow 3\widehat {{O_1}} = {180^0} \Rightarrow \widehat {{O_1}} = {{180} \over 3} = {60^0} \cr} \)

*\(\widehat {{O_3}} = \widehat {{O_1}} = {60^0}\)  (hai góc đối đỉnh)

\(*\widehat {{O_2}} = 2\widehat {{O_1}} = 2.60 = {120^0}\)

\(*\widehat {{O_4}} = \widehat {{O_2}} = {120^0}\)  (hai góc đối đỉnh).

Loigiahay.com


Bình chọn:
4.1 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 8 trên Tuyensinh247.com cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua