Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7 Luyện tập - Chủ đề 1: Góc tạo bởi các đường thẳng

Bài tập 3 trang 118 Tài liệu dạy – học Toán 7 tập 1


Giải bài tập Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc có số đo là 90o. Chứng tỏ rằng mỗi góc còn lại có số đo đều bằng nhau.

Đề bài

Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc có số đo là 90o. Chứng tỏ rằng mỗi góc còn lại có số đo đều bằng nhau.

Lời giải chi tiết

 

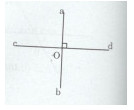
Hai đường thẳng ab và cd cắt nhau tại O và \(\widehat {aOd} = {90^0}\)

Ta có: \(\widehat {aOd} + \widehat {dOb} = {180^0}\)  (hai góc kề bù)

\( \Rightarrow {90^0} + \widehat {dOb} = {180^0} \Rightarrow \widehat {dOb} = {180^0} - {90^0} = {90^0}\)

Góc aOd và bOc là hai góc đối đỉnh \( \Rightarrow \widehat {bOc} = \widehat {aOd} = {90^0}\)

Góc aOc và dOb là hai góc đối đỉnh \( \Rightarrow \widehat {aOc} = \widehat {dOb} = {90^0}\)

Loigiaihay.com


Bình chọn:
3.3 trên 4 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store