-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
Bài 9 trang 87 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho nửa đường tròn (O) có đường kính AB = 2R. Vẽ bán kính OC vuông góc với AB, gọi M là
Đề bài
Cho nửa đường tròn (O) có đường kính AB = 2R. Vẽ bán kính OC vuông góc với AB, gọi M là một điểm nằm trên OC sao cho \(\tan \widehat {OAM} = \dfrac{3}{4}\), AM cắt nửa đường tròn tại D. Tính các đoạn AM, AD, BD theo R.
Phương pháp giải - Xem chi tiết
Sử dụng các tỉ số lượng giác, tỉ lệ đồng dạng và định lý Pythagore để tính.
Lời giải chi tiết
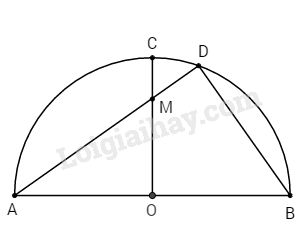
Xét tam gác OAM vuông tại O có:
\(\tan \widehat {OAM} = \dfrac{{OM}}{{OA}} = \dfrac{3}{4} \)
\(\Rightarrow OM = \dfrac{3}{4}OA = \dfrac{3}{4}R\)
Áp dụng định lý Pythagore vào tam giác OAM vuông tại O:
\(A{M^2} = O{A^2} + O{M^2}\)
\(\Rightarrow AM = \sqrt {O{A^2} + O{M^2}} \)\(\, = \sqrt {{R^2} + \dfrac{9}{{16}}{R^2}} = \dfrac{5}{4}R\)
D là một điểm trên nửa đường tròn (O) \( \Rightarrow \widehat {ADB} = {90^o}\) (góc nội tiếp chắn nửa đường tròn)
Xét hai tam giác OAM và DAB có:
+) \(\widehat A\) chung;
+) \(\widehat {AOM} = \widehat {ADB} = {90^o}\)
\( \Rightarrow \)Hai tam giác OAM và DAB đồng dạng
\(\begin{array}{l} \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{{OA}}{{AD}} = \dfrac{{OM}}{{BD}}\\ \Rightarrow AD = \dfrac{{OA.AB}}{{AM}} = \dfrac{{R.2R}}{{\dfrac{5}{4}R}} = \dfrac{8}{5}R\\ BD = \dfrac{{OM.AB}}{{AM}} = \dfrac{{\dfrac{3}{4}R.2R}}{{\dfrac{5}{4}R}} = \dfrac{6}{5}R\end{array}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 10 trang 87 Tài liệu dạy – học Toán 9 tập 1
- Bài 11 trang 87 Tài liệu dạy – học Toán 9 tập 1
- Bài 12 trang 87 Tài liệu dạy – học Toán 9 tập 1
- Bài 13 trang 87 Tài liệu dạy – học Toán 9 tập 1
- Bài 14 trang 87 Tài liệu dạy – học Toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
