Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường ca..

Bài 7 trang 74 Tài liệu dạy – học Toán 9 tập 1


Giải bài tập Cho đường tròn tâm O đường kính AB = 53 cm. C là một điểm trên đường tròn sao cho AC = 45

Đề bài

Cho đường tròn tâm O đường kính AB = 53 cm. C là một điểm trên đường tròn sao cho AC = 45 cm. Gọi H là hình chiếu của C trên AB. Tính BC, AH, BH, CH và OH.

Phương pháp giải - Xem chi tiết

+) Sử dụng định lý về góc nội tiếp chắn nửa đường tròn để chứng minh tam giác ABC vuông tại C từ đó áp dụng định lý Pythagore và hệ thức lượng trong tam giác vuông để tính BC, AH, BH, CH.

+) Áp dụng định lý Pythagore vào tam giác OHC vuông tại H để tính OH.

Lời giải chi tiết

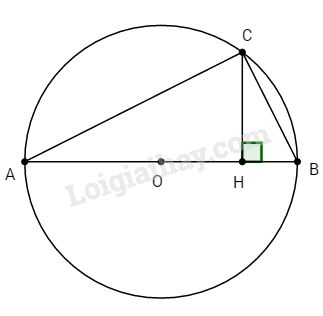
Ta có C là một điểm trên đường tròn tâm O đường kính AB

\( \Rightarrow \widehat {ACB} = {90^o}\) (góc nội tiếp chắn nửa đường tròn)

Áp dụng định lý Pythagore vào tam giác ABC vuông tại C:

\(B{C^2} = A{B^2} - A{C^2} \)\(\,= {53^2} - {45^2} = 784 \)

\(\Rightarrow BC = 28\) (cm)

H là hình chiếu của C trên AB \( \Rightarrow CH \bot AB\)

Áp dụng hệ thức lượng trong tam giác vuông ABC đường cao CH:

\(A{C^2} = AH.AB\)

\(\Rightarrow AH = \dfrac{{A{C^2}}}{{AB}} = \dfrac{{{{45}^2}}}{{53}} = \dfrac{{2025}}{{53}}\) (cm)

\(BH = AB - AH = 53 - \dfrac{{2025}}{{53}}\)\(\, = \dfrac{{784}}{{53}}\)(cm)

\(C{H^2} = AH.BH = \dfrac{{2025}}{{53}}.\dfrac{{784}}{{53}} \)\(\,= \dfrac{{{{45}^2}{{.28}^2}}}{{{{53}^2}}} \)

\(\Rightarrow CH = \dfrac{{1260}}{{53}}\) (cm)

Có đường tròn tâm O đường kính AB = 53 cm \( \Rightarrow \) bán kính R = \(\dfrac{{53}}{2}\) cm

Áp dụng định lý Pythagore vào tam giác OHC vuông tại H:

\(O{H^2} = O{C^2} - C{H^2} \)\(\,= {\left( {\dfrac{{53}}{2}} \right)^2} - \dfrac{{{{45}^2}{{.28}^2}}}{{{{53}^2}}} \)

\(\Rightarrow OH = \dfrac{{1241}}{{106}}\)(cm)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store