Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Luyện tập - Chủ đề 2 : Góc chắn cung

Bài 33 trang 96 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Từ điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB đến đường tròn O (A, B là hai

Đề bài

Từ điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB đến đường tròn O (A, B là hai tiếp điểm). Gọi H là giao điểm của OM và AB.

a) Chứng minh \(M{A^2} = MO.MH\) .

b) Vẽ cát tuyến MCD của (O), C nằm giữa hai điểm M và D.

Chứng minh MO.MH = MC.MD

c) Gọi N là trung điểm của CD. Chứng minh NM là tia phân giác của góc ANB.

d) Tia BN cắt đường tròn O tại K. Chứng minh AK // CD.

Phương pháp giải - Xem chi tiết

a) Áp dụng hệ thức lượng trong tam giác vuông.

b) Chứng minh tam giác MAC và MDC đồng dạng.

c) Chứng minh 5 điểm A, N, O, B, M cùng thuộc đường tròn đường kính OM, sử dụng tính chất góc nội tiếp cùng chắn 1 cung thì bằng nhau, chứng minh hai góc \(\widehat {ANM}\) và \(\widehat {BNM}\) cùng bằng một số góc trung gian.

d) Chứng minh \(\widehat {AKB}\) và \(\widehat {KND}\) cùng bằng nửa số đo cung nhỏ AB của đường tròn \(\left( O \right)\).

Lời giải chi tiết

 

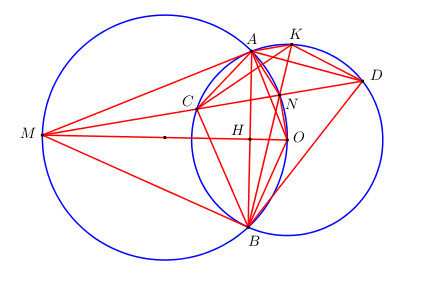
a) Ta có \(MA = MB \Rightarrow M\) thuộc trung trực của AB

\(OA = OB = R \Rightarrow O\)thuộc trung trực của AB

\( \Rightarrow OM\) là trung trực của AB \( \Rightarrow OM \bot AB\) tại H.

Áp dụng hệ thức lượng trong tam giác vuông OAM có: \(M{A^2} = MO.MH\)  (1).

b) Xét tam giác MAC và tam giác MDA có:

\(\widehat {AMC}\) chung;

\(\widehat {MAC} = \widehat {MDA}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung);

\( \Rightarrow \Delta MAC \sim \Delta MDA\,\,\left( {g.g} \right)\)

\(\Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MC}}{{MA}} \Rightarrow M{A^2} = MC.MD\)   (2).

Từ (1) và (2) \( \Rightarrow MO.MH = MC.MD\).

c) Vì N là trung điểm của CD \( \Rightarrow ON \bot CD\) (quan hệ vuông góc giữa đường kính và dây cung).

Ta có: \(\widehat {OAM} = \widehat {ONM} = \widehat {OBM} = {90^0} \Rightarrow A,\,N,\,B\) thuộc đường tròn đường kính OM.

Gọi I là trung điểm của OM \( \Rightarrow \) I là tâm đường tròn đường kính OM.

Xét đường tròn đường kính OM có: \(\widehat {BNM} = \widehat {BOM}\) (1) (hai góc nội tiếp cùng chắn cung BM).

\(\widehat {ANM} = \widehat {ABM}\)(2) (hai góc nội tiếp cùng chắn cung AM).

Ta có: \(\widehat {ABM} + \widehat {OBH} = \widehat {OBM} = {90^0};\,\,\widehat {BOM} + \widehat {OBH} = {90^0}\)

\( \Rightarrow \widehat {ABM} = \widehat {BOM}\)   (3)

Từ (1), (2) và (3) \( \Rightarrow \widehat {ANM} = \widehat {BNM} \Rightarrow NM\) là tia phân giác của \(\widehat {ANB}\).

d) Ta có \(\widehat {ANM} = \widehat {BNM}\,\,\left( {cmt} \right)\). Mà \(\widehat {BNM} = \widehat {KND}\) (đối đỉnh) \( \Rightarrow \widehat {ANM} = \widehat {KND}\).

Xét đường tròn đường kính OM ta có : \(\widehat {ANM} = \widehat {AOM}\) (hai góc nội tiếp cùng chắn cung AM).

Mà OM là đường phân giác của \(\widehat {AOB}\) (tính chất 2 tiếp tuyến cắt nhau)

\( \Rightarrow \widehat {AOM} = \dfrac{1}{2}\widehat {AOB} \)

\(\Rightarrow \widehat {ANM} = \dfrac{1}{2}\widehat {AOB} \)

\(\Rightarrow \widehat {KND} = \dfrac{1}{2}\widehat {AOB} = \dfrac{1}{2}sdcung\,AB\) (số đo góc ở tâm bằng số đo cung bị chắn).

Xét đường tròn \(\left( O \right)\) có \(\widehat {AKB} = \dfrac{1}{2}sdcung\,AB\)  (góc nội tiếp bằng nửa số đo cung bị chắn) \( \Rightarrow \widehat {AKB} = \widehat {KND}\).

Mà hai góc này ở vị trí so le trong \( \Rightarrow AK//CD\).

 Loigiaihay.com


Bình chọn:
3.8 trên 4 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store