-
CHƯƠNG I : CĂN BẬC HAI - CĂN BẬC BA
-
CHƯƠNG II : HÀM SỐ BẬC NHẤT
-
CHƯƠNG III: HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG IV: HÀM SỐ BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI
-
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- 1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
- 2. Hệ thức giữa ba cạnh của tam giác vuông
- 3. Hệ thức giữa đường cao ứng với cạnh huyền và hình chiếu của hai cạnh góc vuông trên cạnh huyền
- 4. Hệ thức diện tích
- 5. Hệ thức giữa đường cao và hai cạnh góc vuông
- Bài tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Luyện tập - Chủ đề 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- 1. Khái niệm tỉ số lượng giác của một góc nhọn
- 2. Liên hệ giữa các tỉ số lượng giác của một góc
- 3. Tỉ số lượng giác của hai góc phụ nhau
- 4. Tỉ số lượng giác của các góc đặc biệt
- 5. Tìm tỉ số lượng giác bằng máy tính cầm tay
- Bài tập - Chủ đề 2 : Tỉ số lượng giác của góc nhọn
- Luyện tập – Chủ đề 2 : Tỉ số lượng giác của góc nhọn
-
Chủ đề 3: Hệ thức về cạnh và góc trong tam giác vuông
-
Chủ đề 4 : Ứng dụng của tỉ số lượng giác
-
Ôn tập chương 1 - Hình học 9
-
-
CHƯƠNG II : ĐƯỜNG TRÒN
-
CHƯƠNG III: GÓC VỚI ĐƯỜNG TRÒN
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Luyện tập - Chủ đề 2 : Góc chắn cung
Bài 24 trang 96 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho tam giác ABC cân tại A
Đề bài
Cho tam giác ABC cân tại A và \(\widehat A = {50^o}\). Nửa đường tròn đường kính AC cắt AB tại D và cắt BC tại H. Tính số đo các cung AD, DH và HC.
Phương pháp giải - Xem chi tiết
+) Chứng minh tam giác ADC vuông tại D, sử dụng định lí đường trung tuyến trong tam giác vuông, chứng minh tam giác OAD cân tại O, tính \(\widehat {AOD}\).
+) Tương tự tính \(\widehat {HOC}\). Từ đó tính \(\widehat {DOH}\).
+) Sử dụng định lí: Số đo góc ở tâm bằng số đo cung bị chắn tính số đo các cung AD, DH và HC.
Lời giải chi tiết
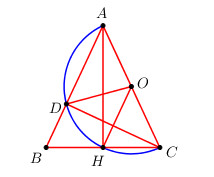
Gọi O là trung điểm AC \( \Rightarrow O\) là tâm đường tròn đường kính AC.
+) Ta có \(\widehat {ADC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ACD\) vuông tại D.
\( \Rightarrow DO = \dfrac{1}{2}AC = OC = OD\) (định lí đường trung tuyến trong tam giác vuông)
\( \Rightarrow \Delta OAD\) cân tại O \( \Rightarrow \widehat {OAD} = \widehat {ODA} = {50^0}\).
Xét tam giác OAD có \(\widehat {OAD} + \widehat {ODA} + \widehat {AOD} = {180^0}\) (tổng ba góc trong một tam giác)
\( \Rightarrow {50^0} + {50^0} + \widehat {AOD} = {180^0} \)
\(\Rightarrow {100^0} + \widehat {AOD} = {180^0} \)
\(\Rightarrow \widehat {AOD} = {180^0} - {100^0} = {80^0}\).
Mà \(\widehat {AOD}\) là góc ở tâm \( \Rightarrow \widehat {AOD} = sdcung\,AD\) (số đo góc ở tâm bằng số đo cung bị chắn).
Vậy \(sd \;cung AD = 80^o\).
+) \(\Delta ABC\) cân tại A \( \Rightarrow \widehat {ABC} = \widehat {ACB}\).
Mà \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = {180^0}\) (tổng ba góc trong 1 tam giác)
\( \Rightarrow \widehat {ABC} + \widehat {ACB} = {180^0} - \widehat {BAC} = {180^0} - {50^0} = {130^0}\).
\( \Rightarrow \widehat {ABC} = \widehat {ACB} = \dfrac{{{{130}^0}}}{2} = {65^0}.\)
Ta có \(\widehat {AHC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta AHC\) vuông tại H.
\( \Rightarrow HO = \dfrac{1}{2}AC = OA = OC\) (định lí đường trung tuyến trong tam giác vuông)
\( \Rightarrow \Delta OHC\) cân tại O \( \Rightarrow \widehat {OHC} = \widehat {OCH} = {65^0}\).
Xét tam giác OHC có : \(\widehat {OCH} + \widehat {OHC} + \widehat {HOC} = {180^0}\) (tổng ba góc trong 1 tam giác).
\( \Rightarrow {65^0} + {65^0} + \widehat {HOC} = {180^0} \)
\(\Rightarrow {130^0} + \widehat {HOC} = {180^0} \)
\(\Rightarrow \widehat {HOC} = {50^0}\).
\( \Rightarrow sdcung\,HC = \widehat {HOC} = {50^0}\) (số đo góc ở tâm bằng số đo cung bị chắn).
+) Ta có :
\(\begin{array}{l}\widehat {AOD} + \widehat {DOH} + \widehat {HOC} = \widehat {AOC} = {180^0} \\\Rightarrow {80^0} + \widehat {DOH} + {50^0} = {180^0}\\ \Rightarrow \widehat {DOH} = {180^0} - {130^0} = {50^0}\end{array}\)
\( \Rightarrow sdcung\,DH = \widehat {DOH} = {50^0}\)(số đo góc ở tâm bằng số đo cung bị chắn).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 25 trang 96 Tài liệu dạy – học Toán 9 tập 2
- Bài 26 trang 96 Tài liệu dạy – học Toán 9 tập 2
- Bài 27 trang 96 Tài liệu dạy – học Toán 9 tập 2
- Bài 28 trang 96 Tài liệu dạy – học Toán 9 tập 2
- Bài 29 trang 96 Tài liệu dạy – học Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
