-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
3. Những hằng đẳng thức đáng nhớ
Hoạt động 7 trang 13 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho một hình vuông có cạnh là a – b (với a > b > 0).
Đề bài
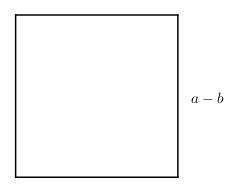
Cho một hình vuông có cạnh là a – b (với \(a > b > 0\)).
a) Hãy viết các biểu thức tính diện tích hình vuông.
b) Từ \({(a - b)^2} = {{\rm{[}}a + ( - b){\rm{]}}^2}\) , hãy khai triển biểu thức ở câu a.
c) Tính diện tích hình vuông bằng cách thế a = 5, b = 3 vào biểu thức ở câu a và biểu thức được khai triển ở câu b.
Lời giải chi tiết
a) Diện tích hình vuông \(\left( {a - b} \right)\left( {a - b} \right) = {\left( {a - b} \right)^2}\)
b) \({\left( {a - b} \right)^2} = {\left[ {a + \left( { - b} \right)} \right]^2} = {a^2} + 2a\left( { - b} \right) + 2a\left( { - b} \right) + {\left( { - b} \right)^2} = {a^2} - 2ab + {b^2}\)
c) Diện tích hình vuông là : \({\left( {5 - 3} \right)^2} = {2^2} = 4\) và cũng là \({5^2} - 2.5.3 + {3^2} = 25 - 30 + 9 = 4\)
Loigiaihay.com
Bình luận
Chia sẻ
- Hoạt động 8 trang 13 Tài liệu dạy – học Toán 8 tập 1.
- Hoạt động 9 trang 13 Tài liệu dạy –học Toán 8 tập 1
- Thử tài bạn trang 14 Tài liệu dạy – học Toán 8 tập 1
- Thử tài bạn trang 14(2) Tài liệu dạy – học Toán 8 tập 1
- Hoạt động 10 trang 14 Tài liệu dạy – học Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
