-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 9.1, 9.2, 9.3 phần bài tập bổ sung trang 51, 52 SBT toán 7 tập 2
Bài 9.1, 9.2, 9.3 phần bài tập bổ sung trang 51, 52 sách bài tập toán 7. Hãy chọn khẳng định đúng trong các khẳng định sau: (A) Trực tâm của một tam giác bao giờ cũng nằm trong tam giác...
Bài 9.1
Hãy chọn khẳng định đúng trong các khẳng định sau:
(A) Trực tâm của một tam giác bao giờ cũng nằm trong tam giác.
(B) Trực tâm của một tam giác bao giờ cũng nằm ngoài tam giác.
(C) Trực tâm của một tam giác bao giờ cũng trùng với một đỉnh của tam giác.
(D) Cả ba khẳng định trên đều sai.
Phương pháp giải:
Sử dụng: Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác
Lời giải chi tiết:
Trực tâm của tam giác nằm trong tam giác chỉ với tam giác nhọn, nằm ngoài tam giác chỉ với tam giác tù, trùng với một đỉnh của tam giác chỉ với tam giác vuông.
Vậy cả ba khẳng định A, B, C đều sai.
Chọn (D)
Bài 9.2
Cho tam giác \(ABC\) không là tam giác cân. Khi đó trực tâm của tam giác \(ABC\) là giao điểm của:
(A) Ba đường trung tuyến;
(B) Ba đường phân giác;
(C) Ba đường trung trực;
(D) Ba đường cao.
Hãy chọn phương án đúng.
Phương pháp giải:
Sử dụng: Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác
Lời giải chi tiết:
Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.
Chọn (D)
Bài 9.3
Cho tam giác \(ABC\) có hai đường cao \(AH, BK\) cắt nhau tại điểm \(M.\) Hãy tính góc \(AMB\) biết \(Â = 55°,\) \(\widehat B = 67^\circ \).
Phương pháp giải:
Sử dụng:
+) Trong tam giác vuông, tổng hai góc nhọn bằng \(90^0\)
+) Tổng ba góc trong tam giác bằng \(180^0\)
Lời giải chi tiết:
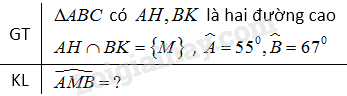
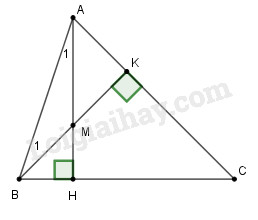
Để tính góc \(AMB,\) ta cần tính \(\widehat {{A_1}},\widehat {{B_1}}\)
Trong tam giác vuông \(AHB\) có \(\widehat {{A_1}} + \widehat {ABH}= 90^\circ \) (tổng hai góc nhọn trong tam giác vuông bằng \(90^0)\) nên \(\widehat {{A_1}} = 90^\circ - \widehat {ABH} \)\(= 90^\circ - 67^\circ = 23^\circ \)
Trong tam giác vuông \(AKB\) có \(\widehat {{B_1}} + \widehat {BAK}= 90^\circ \) (tổng hai góc nhọn trong tam giác vuông bằng \(90^0)\) nên \(\widehat {{B_1}} = 90^\circ - \widehat {BAK} \)\(= 90^\circ - 55^\circ = 35^\circ \)
Trong tam giác \(AMB\) có \(\widehat {AMB} + {\widehat {{A_1}} + \widehat {{B_1}}} = 180^\circ \) (định lý tổng ba góc trong tam giác) nên \(\widehat {AMB} = 180^\circ - \left( {\widehat {{A_1}} + \widehat {{B_1}}} \right) \)\(\;= 180^\circ - (23^\circ + 35^\circ ) = 122^\circ \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9.4, 9.5, 9.6 phần bài tập bổ sung trang 52 SBT toán 7 tập 2
- Bài 81* trang 51 SBT toán 7 tập 2
- Bài 80 trang 51 SBT toán 7 tập 2
- Bài 79 trang 51 SBT toán 7 tập 2
- Bài 78 trang 51 SBT toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
