-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 7.4, 7.5, 7.6 phần bài tập bổ sung trang 49 SBT toán 7 tập 2
Bài 7.4, 7.5, 7.6 phần bài tập bổ sung trang 49 sách bài tập toán 7. Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng:a) D là trung điểm của cạnh BC...
Bài 7.4
Trong tam giác \(ABC,\) hai đường trung trực của hai cạnh \(AB\) và \(AC\) cắt nhau tại điểm \(D\) nằm trên cạnh \(BC.\) Chứng minh rằng:
a) \(D\) là trung điểm của cạnh \(BC.\)
b) \(\widehat A = \widehat B + \widehat C\)
Phương pháp giải:
Sử dụng:
+) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó
+) Tính chất tam giác cân
Lời giải chi tiết:
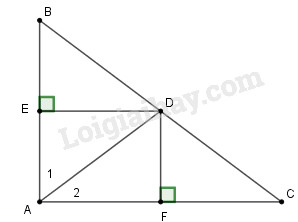
a) Vì \(D\) thuộc đường trung trực cạnh \(AB\) nên \(DB=DA\) (tính chất)
Vì \(D\) thuộc đường trung trực cạnh \(AC\) nên \(DC=DA\) (tính chất)
Suy ra \(DB=DC\,(=DA)\) hay \(D\) là trung điểm cạnh \(BC.\)
b) Vì \(DA=DB \) (chứng minh trên) nên tam giác \(DAB\) cân tại \(D.\) Suy ra \(\widehat B = \widehat {{A_1}}\).
Vì \(DA=DC \) (chứng minh trên) nên tam giác \(DAC\) cân tại \(D.\) Suy ra \(\widehat C = \widehat {{A_2}}\).
Do đó: \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = \widehat B + \widehat C\)
Bài 7.5
Chứng minh rằng nếu trong tam giác \(ABC\) có hai cạnh \(AB\) và \(AC\) không bằng nhau thì đường trung tuyến xuất phát từ đỉnh \(A\) không vuông góc với \(BC.\)
Phương pháp giải:
Sử dụng:
+) Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó
Lời giải chi tiết:
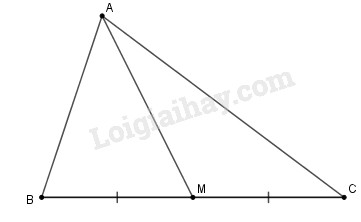
Gọi \(AM\) là đường trung tuyến xuất phát từ đỉnh \(A\) của tam giác \(ABC.\)
Vì \(AM\) là đường trung tuyến của tam giác \(ABC\) nên \(M\) là trung điểm của cạnh \(BC.\)
Giả sử \(AM \bot BC\). Khi đó \(AM\) là đường trung trực của đoạn thẳng \(BC.\) Suy ra \(AB = AC.\)
Điều này mâu thuẫn với giả thiết \(AB\) không bằng \(AC.\) Vậy trung tuyến \(AM\) không vuông góc với \(BC.\)
Bài 7.6
Cho đường thẳng \(d\) và hai điểm \(A, B\) nằm về một phía của \(d\) sao cho \(AB\) không vuông góc với \(d.\) Hãy tìm trên \(d\) một điểm \(M\) sao cho \(\left| {MA - MB} \right|\) có giá trị nhỏ nhất.
Phương pháp giải:
Sử dụng: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó
Lời giải chi tiết:
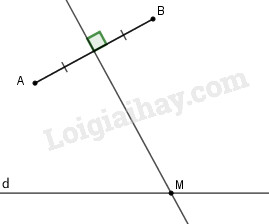
Ta có \(\left| {MA - MB} \right| \ge 0\) với một điểm \(M\) tùy ý và \(\left| {MA - MB} \right| = 0\) với các điểm \(M\) thỏa mãn \(MA = MB.\) Khi \(MA=MB\) thì các điểm \(M\) nằm trên đường trung trực của đoạn thẳng \(AB.\)
Mặt khác \(M\) phải thuộc \(d.\) Vậy \( M\) là giao điểm của đường thẳng \(d\) và đường trung trực của đoạn thẳng \(AB\) (tồn tại giao điểm này vì \(AB\) không vuông góc với \(d.)\)
Tóm lại: Khi \(M\) là giao điểm của \(d\) và đường trung trực của đoạn thẳng \(AB\) thì \(\left| {MA - MB} \right|\) đạt giá trị nhỏ nhất là bằng \(0.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 7.1, 7.2, 7.3 phần bài tập bổ sung trang 48, 49 SBT toán 7 tập 2
- Bài 63 trang 48 SBT toán 7 tập 2
- Bài 62 trang 48 SBT toán 7 tập 2
- Bài 61 trang 48 SBT toán 7 tập 2
- Bài 60 trang 48 SBT toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
