Bài 64 trang 49 SBT toán 7 tập 2

Giải bài 64 trang 49 sách bài tập toán 7. Cho tam giác ABC. Tìm một điểm O cách đều ba điểm A, B, C.

Đề bài

Cho tam giác \(ABC.\) Tìm một điểm \(O\) cách đều ba điểm \(A, B, C.\)

Phương pháp giải - Xem chi tiết

Sử dụng:

+) Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

+) Ba đường trung trực của tam giác cắt nhau tại 1 điểm.

Lời giải chi tiết

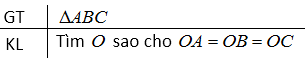
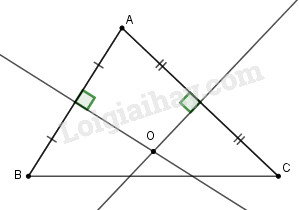
Điểm \(O\) cách đều hai điểm \(A\) và \(B\)

\( \Rightarrow O\) thuộc đường trung trực của \(AB.\)

Điểm \(O\) cách đều hai điểm \(A\) và \(C\)

\( \Rightarrow O\) thuộc đường trung trực \(AC.\)

Điểm \(O\) cách đều hai điểm \(B \) và \(C\)

\( \Rightarrow O\) thuộc đường trung trực của \(BC.\)

Như vậy \(O\) là giao của ba đường trung trực tam giác \(ABC.\)

Trong một tam giác, ba đường trung trực đồng quy tại một điểm, nên ta dựng đường trung trực \(AB\) và \(AC\) cắt nhau tại \(O.\)

Điểm \(O\) là điểm cần tìm.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 11 phiếu

Bài tiếp theo

Bài 65 trang 49 SBT toán 7 tập 2
Giải bài 65 trang 49 sách bài tập toán 7. Chứng minh rằng ba điểm B, K, C thẳng hàng.
Bài 66 trang 49 SBT toán 7 tập 2
Giải bài 66 trang 49 sách bài tập toán 7. Dựa vào kết quả của bài 65, chứng minh rằng: a) Các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.
Bài 67 trang 50 SBT toán 7 tập 2
Giải bài 67 trang 50 sách bài tập toán 7. Hãy nêu cách xác định tâm của đường viền.Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gẫy (hình bên). Hãy nêu cách xác định tâm của đường viền.
Bài 68 trang 50 SBT toán 7 tập 2
Giải bài 68 trang 50 sách bài tập toán 7. Cho tam giác ABC cân tại A, đường trung tuyến AM. Đường trung trực của AC cắt đường thẳng AM ở D. Chứng minh rằng DA = DB.
Bài 69 trang 50 SBT toán 7 tập 2
Giải bài 69 trang 50 sách bài tập toán 7. Cho tam giác ABC có Â là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E...
Bài 8.1, 8.2, 8.3, 8.4 phần bài tập bổ sung trang 50 SBT toán 7 tập 2
Giải bài 8.1, 8.2, 8.3, 8.4 phần bài tập bổ sung trang 50 sách bài tập toán 7. Cho tam giác cân (không đều) ABC có AB = AC. Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Khi đó khẳng định nào sau đây là đúng?...