Giải bài tập, Sách bài tập (SBT) Toán 7

Bài 7. Định lí Py-ta-go

Bài 7.1, 7.2, 7.3 phần bài tập bổ sung trang 150, 151 SBT toán 7 tập 1

Giải bài 7.1, 7.2, 7.3 phần bài tập bổ sung trang 150, 151 sách bài tập toán 7 tập 1. Độ dài x trên hình bs 5 bằng ...

Lựa chọn câu để xem lời giải nhanh hơn

Bài 7.1

Độ dài \(x\) trên hình bs 5 bằng

(A) \(\sqrt {69} \); (B) \(10\);

Hãy chọn phương án đúng.

Phương pháp giải:

Áp dụng định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.

Lời giải chi tiết:

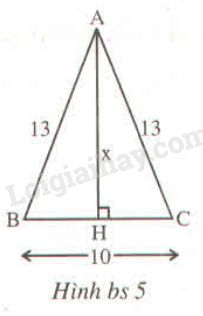
\(\Delta ABC\) có \(AB=AC=13\) nên \(\Delta ABC\) cân tại \(A\).

\( \Rightarrow \widehat B = \widehat C\) (tính chất tam giác cân)

Xét \(\Delta ABH\) và \(\Delta ACH\) có:

\(AB=AC=13\)

\( \widehat B = \widehat C\) (chứng minh trên)

\(\widehat {AHB} = \widehat {AHC}=90^o\)

\( \Rightarrow \Delta ABH = \Delta ACH\) (cạnh huyền - góc nhọn).

\( \Rightarrow BH = CH\) (hai cạnh tương ứng)

\( \Rightarrow H\) là trung điểm cạnh BC

\( \Rightarrow BH = BC:2 = 10:2 = 5\) (đơn vị độ dài).

Áp dụng định lí Pytago vào \(\Delta AHB\) vuông tại \(H\), ta có:

\(\begin{array}{l}
A{B^2} = A{H^2} + B{H^2}\\
\Rightarrow A{H^2} = A{B^2} - B{H^2}\\
\Rightarrow A{H^2} = {13^2} - {5^2} = 144\\
\Rightarrow AH = 12
\end{array}\)

Chọn D.

Bài 7.2

Một tam giác vuông có các cạnh góc vuông tỉ lệ với \(7\) và \(24\), chu vi bằng \(112 cm.\) Tính độ dài cạnh huyền.

Phương pháp giải:

Áp dụng định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.

Lời giải chi tiết:

Gọi \(b, c\,(cm)\) là độ dài các cạnh góc vuông, \(a\,(cm)\) là độ dài cạnh huyền \(\left( {112 > a>b,c > 0} \right)\).

Theo đề bài ta có: \(\dfrac{b}{7} = \dfrac{c}{{24}}\)

Đặt:

\(\begin{array}{l}
\dfrac{b}{7} = \dfrac{c}{{24}} = k\,\left( {k > 0} \right)\\
\Rightarrow b = 7k;\,c = 24k
\end{array}\)

Áp dụng định lí Py-ta-go vào tam giác vuông, ta có:

\(\begin{array}{l}
{a^2} = {b^2} + {c^2}\\
\Rightarrow {a^2} = {\left( {7k} \right)^2} + {\left( {24k} \right)^2} = 625{k^2}\\
\Rightarrow a = \sqrt {625{k^2}} = 25k
\end{array}\)

Chu vi của tam giác bằng \(112 cm\) nên ta có:

\(a + b + c = 112 \)

\(\begin{array}{l}
\Rightarrow 25k + 7k + 24k = 112\\
\Rightarrow 56k = 112\\
\Rightarrow k = 112:56 = 2\text{(thỏa mãn)}
\end{array}\)

\( \Rightarrow a = 25.2 = 50\,\left( {cm} \right)\)

Vậy cạnh huyền có độ dài là \(50\,cm.\)

Bài 7.3

Tìm số tự nhiên \(a\), biết rằng \(a, 8, 15\) là độ dài ba cạnh của một tam giác vuông.

Phương pháp giải:

Áp dụng định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.

Lời giải chi tiết:

- Trường hợp 1: \( a\) là độ dài một cạnh góc vuông.

Áp dụng định lí Pytago ta có:

\(\begin{array}{l}
{a^2} + {8^2} = {15^2}\\
\Rightarrow {a^2} = {15^2} - {8^2} = 161\\
\Rightarrow a = \sqrt {161}
\end{array}\)

\(a\) không là số tự nhiên nên trường hợp này không thỏa mãn.

- Trường hợp 2: \( a\) là độ dài cạnh huyền.

Áp dụng định lí Pytago ta có:

\(\begin{array}{l}
{a^2} = {8^2} + {15^2} = 289\\
\Rightarrow a = \sqrt {289} = 17\text{ (thỏa mãn)}
\end{array}\)

Vậy \(a=17.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.6 trên 7 phiếu

Bài tiếp theo

Bài 92 trang 150 SBT toán 7 tập 1
Giải bài 92 trang 150 sách bài tập toán 7 tập 1. Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông (hình 67) là tam giác vuông cân.
Bài 91 trang 150 SBT toán 7 tập 1
Giải bài 91 trang 150 sách bài tập toán 7 tập 1. Cho các số: 5; 8; 9; 12; 13; 15; 17. Hãy chọn ra các bộ ba có thể là độ dài ba cạnh của một tam giác vuông.
Bài 90 trang 150 SBT toán 7 tập 1
Giải bài 90 trang 150 sách bài tập toán 7 tập 1. Bạn An đi từ nhà mình (A) qua nhà bạn Bảo (B) rồi đến nhà bạn Châu (C)...
Bài 89 trang 150 SBT toán 7 tập 1
Giải bài 89 trang 150 sách bài tập toán 7 tập 1. Tính cạnh đáy BC của tam giác cân ABC trên các hình 64, 65...
Bài 88 trang 150 SBT toán 7 tập 1
Giải bài 88 trang 150 sách bài tập toán 7 tập 1. Tính độ dài các cạnh góc vuông của một tam giác vuông cân có cạnh huyền bằng 2cm ...
Bài 87 trang 149 SBT toán 7 tập 1
Giải bài 87 trang 149 sách bài tập toán 7 tập 1. Hai đoạn thẳng AC, BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn thẳng....
Bài 86 trang 149 SBT toán 7 tập 1
Giải bài 86 trang 149 sách bài tập toán 7 tập 1. Tính đường chéo của một mặt bàn hình chữ nhật có chiều dài 10dm, chiều rộng 5dm.
Bài 85 trang 149 SBT toán 7 tập 1
Giải bài 85 trang 149 sách bài tập toán 7 tập 1. Màn hình của một máy thu hình có dạng hình chữ nhật, chiều rộng 12 inh-sơ, đường chéo 20 inh-sơ. Tính chiều dài.
Bài 84 trang 149 SBT toán 7 tập 1
Giải bài 84 trang 149 sách bài tập toán 7 tập 1. Tính độ dài các đoạn thẳng AB, BC, CD, DA trên hình 63.
Bài 83 trang 149 SBT toán 7 tập 1
Giải bài 83 trang 149 sách bài tập toán 7 tập 1. Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AC = 20cm, AH = 12cm, BH = 5cm.
Bài 82 trang 149 SBT toán 7 tập 1
Giải bài 82 trang 149 sách bài tập toán 7 tập 1. Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13cm, cạnh góc vuông kia bằng 12cm.