-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 61 trang 87 SBT toán 8 tập 1
Giải bài 61 trang 87 sách bài tập toán 8. Cho tam giác nhọn ABC có A = 60 độ, trực tâm H. Gọi M là điểm đối xứng với H qua BC. a) Chứng minh ∆ BHC = ∆ BMC...
Đề bài
Cho tam giác nhọn \(ABC\) có \(\widehat A = {60^0}\), trực tâm \(H.\) Gọi \(M\) là điểm đối xứng với \(H\) qua \(BC.\)
\(a)\) Chứng minh \(∆ BHC = ∆ BMC.\)
\(b)\) Tính \(\widehat {BMC}\)
Phương pháp giải - Xem chi tiết
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Tổng bốn góc của một tứ giác bằng \(360^o.\)
Lời giải chi tiết
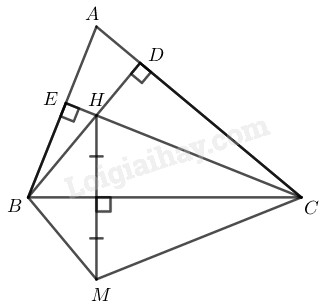
\(a)\) Vì \(M\) đối xứng với \(H\) qua trục \(BC\)
\(⇒ BC\) là đường trung trực của \(HM\)
\(⇒ BH = BM\) ( tính chất đường trung trực)
\(CH = CM\) ( tính chất đường trung trực)
Xét tam giác \(BHC\) và tam giác \(BMC\) có:
Cạnh \(BC\) chung
\(BH= BM\) ( chứng minh trên)
\(CH = CM\) (chứng minh trên)
Suy ra: \(∆ BHC = ∆ BMC \;\; (c.c.c)\)
\(b)\) Gọi giao điểm \(BH\) với \(AC\) là \(D,\) giao điểm của \(CH\) và \(AB\) là \(E\)
\(H\) là trực tâm của \(∆ ABC\)
\(⇒ BD ⊥ AC, CE ⊥ AB\)
+) Xét tứ giác \(ADHE\) ta có:
\(\widehat {DHE} +\widehat A + \widehat D + \widehat E= {360^0} \) (tổng 4 góc trong tứ giác bằng \(360^0)\)
\(\Rightarrow \widehat {DHE} = {360^0} - \left( {\widehat A + \widehat D + \widehat E} \right) \)
\(= {360^0} - \left( {{{60}^0} + {{90}^0} + {{90}^0}} \right) = {120^0}\) (1)
+) Mà \(\widehat {BHC} = \widehat {DHE}\) (đối đỉnh) (2)
+) Vì \(∆ BHC = ∆ BMC\) (chứng minh trên) nên \(\widehat {BMC} = \widehat {BHC}\) ( 2 góc tương ứng) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {BMC} = \widehat {DHE} = {120^0}\)
Bình luận
Chia sẻ
- Bài 62 trang 87 SBT toán 8 tập 1
- Bài 63 trang 87 SBT toán 8 tập 1
- Bài 64 trang 87 SBT toán 8 tập 1
- Bài 65 trang 87 SBT toán 8 tập 1
- Bài 66 trang 87 SBT toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
