-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 4.1 phần bài tập bổ sung trang 162 SBT toán 8 tập 1
Giải bài 4.1 phần bài tập bổ sung trang 162 sách bài tập toán 8. Tính diện tích của hình được cho trong mỗi trường hợp sau:
Tính diện tích của hình được cho trong mỗi trường hợp sau:
LG a
Hình thang \(ABCD,\) đáy lớn \(AB = 10\,cm,\) đáy nhỏ \(CD = 6\,cm\) và đường cao \(DE = 5\,cm.\)
Phương pháp giải:
Áp dụng công thức tính diện tích hình thang bằng tích của nửa tổng hai đáy với chiều cao: \(S=\dfrac{a+b}{2}.h\)
Lời giải chi tiết:
Áp dụng công thức tính diện tích hình thang.
\(S=\dfrac{a+b}{2}.h=\dfrac{10+6}{2}.5\) \(= 40 (c{m^2})\)
LG b
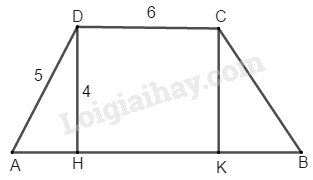
Hình thang cân \(ABCD,\) đáy nhỏ \(CD = 6\,cm,\) đường cao \(DH = 4\,cm\) và cạnh bên \(AD = 5\,cm.\)
Phương pháp giải:
Áp dụng công thức tính diện tích hình thang bằng tích của nửa tổng hai đáy với chiều cao: \(S=\dfrac{a+b}{2}.h\)
Lời giải chi tiết:
Xét hình thang cân \(ABCD\) có \(AB // CD\)
Đáy nhỏ \(CD = 6\,cm,\) cạnh bên \(AD = 5\,cm\)
Đường cao \(DH = 4\,cm.\) Kẻ \(CK ⊥ AB\)
Ta có tứ giác \(CDHK\) là hình chữ nhật (vì có \(DC//HK,DH//CK\) (cùng vuông với AB) và \(DH\bot HK\))
Suy ra \(HK = CD = 6\,cm\)
\(∆ AHD\) vuông tại \(H.\) Theo định lý Pi-ta-go ta có: \(A{D^2} = A{H^2} + D{H^2}\)
\( \Rightarrow {\rm A}{{\rm H}^2} = A{D^2} - D{H^2} = {5^2} - {4^2}\\ = 25 - 16 = 9 \Rightarrow AH = 3cm\)
Xét hai tam giác vuông \(DHA\) và \(CKB :\)
\(\widehat {DHA} = \widehat {CKB} = 90^\circ \)
\(AD = BC\) (tính chất hình thang cân)
\(\widehat A = \widehat B\) (do ABCD là hình thang cân)
Do đó: \(∆ DHA = ∆ CKB\) (cạnh huyền, góc nhọn)
\(⇒ KB = AH = 3\, (cm)\)
\(AB = AH + HK + KB \) \(= 3+ 6+ 3 = 12\, (cm)\)
\(S_{ABCD}=\dfrac{AB+CD}{2}.DH\) \(=\dfrac{12+6}{2}.4=36 (c{m^2})\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 4.2 phần bài tập bổ sung trang 162 SBT toán 8 tập 1
- Bài 4.3 phần bài tập bổ sung trang 162 SBT toán 8 tập 1
- Bài 41 trang 162 SBT toán 8 tập 1
- Bài 40 trang 162 SBT toán 8 tập 1
- Bài 39 trang 162 SBT toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
