-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số bậc hai y=ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số bậc hai
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Bài tập ôn chương 4 - Hàm số y=ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài tập ôn chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN – HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 3.2 phần bài tập bổ sung trang 103 SBT toán 9 tập 2
Giải bài 3.2 phần bài tập bổ sung trang 103 sách bài tập toán 9.Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C...
Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD
Đề bài
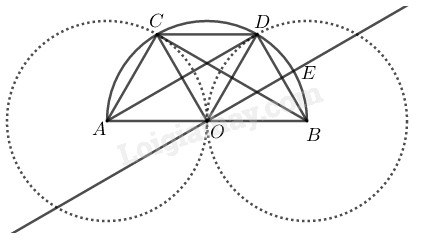
Cho nửa đường tròn đường kính \(AB,\) tâm \(O.\) Đường tròn tâm \(A\) bán kính \(AO\) cắt nửa đường tròn đã cho tại \(C.\) Đường tròn tâm \(B\) bán kính \(BO\) cắt nửa đường tròn đã cho tại \(D.\) Đường thẳng qua \(O\) và song song với \(AD\) cắt nửa đường tròn đã cho tại \(E.\)
\(a)\) \(\widehat {ADC}\) và \(\widehat {ABC}\) có bằng nhau không\(?\) Vì sao\(?\)
\(b)\) Chứng minh \(CD\) song song với \(AB.\)
\(c)\) Chứng minh \(AD\) vuông góc với \(OC\)
\(d)\) Tính số đo của \(\widehat {DAO}\).
\(e)\) So sánh hai cung \(BE\) và \(CD.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+) Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Trong hình thoi, hai đường chéo vuông góc.
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải chi tiết
\(a)\) Trong đường tròn \((O)\) ta có:
\(\widehat {ADC} = \widehat {ABC}\) (\(2\) góc nội tiếp cùng chắn cung \(\overparen{AC}\))
\(b)\) \(∆ACB\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên \(∆ABC\) vuông tại \(C\)
\( \Rightarrow CO = OA = \displaystyle{1 \over 2}AB\) (tính chất tam giác vuông)
Mà \(AC = AO\) (bán kính đường tròn \((A)\))
Suy ra: \(AC = AO = OC\)
\( \Rightarrow \)\( ∆ACO\) đều \( \Rightarrow \widehat {AOC} = {60^o}\)
Ta có: \(∆ADB\) nội tiếp trong đường tròn đường kính \(AB\) nên \(∆ADB\) vuông tại \(D\)
\( \Rightarrow DO = OB = OA = \displaystyle {1 \over 2}AB\) (tính chất tam giác vuông)
\(BD = BO\) (bán kính đường tròn \((B)\))
Suy ra: \(BO = OD = BD\)
\( \Rightarrow \) \(∆BOD\) đều
\( \Rightarrow \widehat {ODB} = \widehat {BOD} = {60^o}\)
Mà \(\widehat {AOC} + \widehat {COD} + \widehat {BOD} = {180^o}\)
Suy ra: \(\widehat {COD} = {60^o}\)
Kết hợp với: \(OC = OD\) (vì cùng bằng \(\displaystyle {1 \over 2}AB\))
Suy ra: \(∆COD\) đều
\( \Rightarrow \widehat {ODC} = {60^o} \Rightarrow \widehat {ODC} = \widehat {BOD}\)
\( \Rightarrow \) \(CD // AB\) (vì có cặp góc ở vị trí so le trong bằng nhau)
\(c)\) Ta có: \(∆AOC\) đều (chứng minh trên) \( \Rightarrow OA = AC = OC\)
\(∆OCD\) đều (chứng minh trên) \( \Rightarrow OC = OD = CD\)
Suy ra: \(AC = AO = OD = DC\)
Vậy: tứ giác \(AODC\) là hình thoi. Suy ra \( AD \bot OC.\)
\(d)\) \(∆BOD\) đều (chứng minh trên) \( \Rightarrow \widehat {OBD} = {60^o}\) hay \(\widehat {ABD} = {60^o}\)
Vì \(∆ADB\) vuông tại \(D\)
\( \Rightarrow \widehat {DAB} + \widehat {ABD} = {90^o}\)
\( \Rightarrow \widehat {DAB} = {90^o} - \widehat {ABD} \)\(= {90^o} - {60^o} = {30^o}\)
Vậy \(\widehat {DAO} = {30^o}\)
\(e)\) \(OE // AD\;\; (gt)\)
\( \Rightarrow \widehat {EOB} = \widehat {DAO} = {30^o}\) (hai góc đồng vị)
\( sđ \overparen{BE}\) \( = \widehat {EOB} = {30^0}\)
\( sđ \overparen{CD}\) \( = \widehat {COD}\)
mà \(\widehat {COD} = {60^o}\) (chứng minh trên)
\( sđ \overparen{CD} = 60^o\)
Suy ra: Số đo cung \(\overparen{CD}\) gấp đôi số đo cung \(\overparen{BE}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3.1 phần bài tập bổ sung trang 103 SBT toán 9 tập 2
- Bài 23 trang 103 SBT toán 9 tập 2
- Bài 22 trang 102 SBT toán 9 tập 2
- Bài 21 trang 102 SBT toán 9 tập 2
- Bài 20 trang 102 SBT toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com, cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
