Bài 2.6, 2.7, 2.8, 2.9, 2.10 trang 98, 99 SBT toán 6 tập 2

Bài II.6

Vẽ \(\widehat {mOn} = 100^\circ \) (h.bs.8). Vẽ tiếp \(\widehat {mOx} = 90^\circ \) và tia \(Ox\) ở trong góc \(mOn\). Vẽ tiếp \(\widehat {mOy} = 10^\circ \) và tia \(Oy\) ở trong góc \(mOn\). Vẽ tiếp \(Oz\) là tia phân giác của góc \(mOn\). Khi đó số đo của góc \(xOz\) bằng bao nhiêu?

(A) \(10^\circ;\)                                       (B) \(40^\circ;\)

(C) \(50^\circ; \)                                       (D) \(80^\circ.\)

Phương pháp giải:

Áp dụng các tính chất : 

+ Trên nửa mặt phẳng bờ chứa tia \(Ox\) có hai tia \(Oy, Oz\) mà \(\widehat{xOy}< \widehat{xOz}\) thì tia \(Oy\) nằm giữa hai tia \(Ox, Oz.\)

+ Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\).

Lời giải chi tiết:

Trên nửa mặt phẳng bờ chứa tia \(Om\) ta có \(\widehat {mOx} < \widehat {mOn}\) \((90^\circ < 100^\circ)\) nên tia \(Ox\) nằm giữa hai tia \(Om\) và \(On\)

\(\Rightarrow \widehat {mOx} + \widehat {xOn} = \widehat {mOn}\)

\(\Rightarrow   \widehat {xOn} = \widehat {mOn} - \widehat {mOx}\)\(=100^\circ - 90^\circ = 10^\circ \)

Vì \(Oz\) là tia phân giác của góc \(mOn\) nên \(\widehat{nOz}=\dfrac{\widehat{mOn}}{2} = \dfrac{100^\circ}{2} = 50^\circ\)

Trên nửa mặt phẳng bờ chứa tia \(On\) ta có \(\widehat {nOx} < \widehat {nOz}\) \((10^\circ < 50^\circ)\) nên tia \(Ox\) nằm giữa hai tia \(On\) và \(Oz\)

\(\Rightarrow \widehat {nOx} + \widehat {xOz} = \widehat {nOz}\)

\(\Rightarrow   \widehat {xOz} = \widehat {nOz} - \widehat {nOx}\)\(=50^\circ - 10^\circ = 40^\circ \)

Chọn đáp án (B) \(40^\circ.\) 

Bài II.7

Biết rằng hai góc \(mOn\) và \(nOp\) kề bù, hơn nữa \(\widehat {mOn} = 5\widehat {nOp}\). Khi đó  

\(\left( A \right)\widehat {mOn} = 30^\circ \), \(\widehat {nOp} = 150^\circ ;\)

\(\left( B \right)\widehat {mOn} = 150^\circ \), \(\widehat {nOp} = 30^\circ ;\)

\(\left( C \right)\widehat {mOn} = 144^\circ \), \(\widehat {nOp} = 36^\circ ;\)

\(\left( D \right)\widehat {mOn} = 36^\circ \), \(\widehat {nOp} = 144^\circ .\)

Phương pháp giải:

Áp dụng định nghĩa : Hai góc kề bù là hai góc kề nhau và có tổng số đo bằng \(180^\circ .\)

Lời giải chi tiết:

Vì hai góc \(mOn\) và \(nOp\) kề bù nên ta có :

\(\widehat {mOn}  + \widehat {nOp} =180^\circ \)

Thay \(\widehat {mOn} = 5\widehat {nOp}\) ta được :

\(5\widehat {nOp} +\widehat {nOp} =180^\circ\)

\(\Rightarrow \widehat {nOp} (5+1)=180^\circ\)

\(\Rightarrow 6.\widehat {nOp} =180^\circ\)

\(\Rightarrow \widehat {nOp} =180^\circ:6\)

\(\Rightarrow \widehat {nOp} =30^\circ\)

\(\Rightarrow \widehat {mOn} = 5\widehat {nOp}=5.30^\circ = 150^\circ.\)

Chọn đáp án \(\left( B \right)\widehat {mOn} = 150^\circ \), \(\widehat {nOp} = 30^\circ .\)

Bài II.8

Trên đường tròn tâm \(O\) bán kính \(R \;(R > 0)\) lấy 5 điểm \(M, N, P, Q, S\). Khi đó số các cung có hai đầu mút lấy trong số các điểm đã cho bằng

(A) \(20; \)                                          (B) \(10;\)

(C) \(40;\)                                          (D) \(200.\)

Phương pháp giải:

Vẽ hình theo yêu cầu đề bài, từ đó xác định các cung có hai đầu mút lấy trong số các điểm đã cho.

Lời giải chi tiết:

Ta có hình vẽ : 

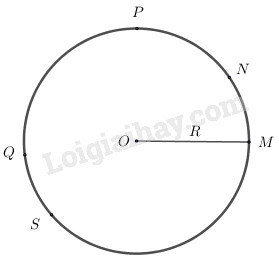
Đếm các cung tạo thành ta có:

Số các cung có hai đầu mút lấy trong số các điểm đã cho là \(20.\)

Hoặc ta sử dụng:

Với \(n\ge 2\) điểm phân biệt trên đường tròn thì tạo thành \(n.(n-1)\) cung tròn.

Từ đó với 5 điểm phân biệt thì số cung tròn tạo thành là \(5.(5-1)=20\) cung. 

Chọn đáp án (A) \(20.\)

Bài II.9

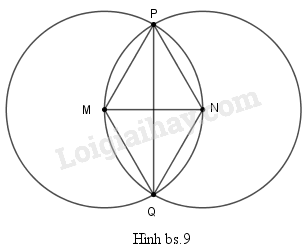
Cho hình bs.9. Khi đó

(A) \(MP = MQ = MN = PQ\)

(B) \(MP = MQ = NQ = NP\)

(C) \(MP = MQ = NP = PQ\)

(D) \(MP = MQ > NQ = NP\)

Phương pháp giải:

Quan sát hình vẽ đã cho để xác định các đoạn thẳng bằng nhau.

Lời giải chi tiết:

Quan sát hình vẽ đã cho ta thấy hai đường tròn bằng nhau nên \(MP = MQ = NQ = NP\) (vì cùng bằng bán kính).

Chọn đáp án (B)  \(MP = MQ = NQ = NP\)

Bài II.10

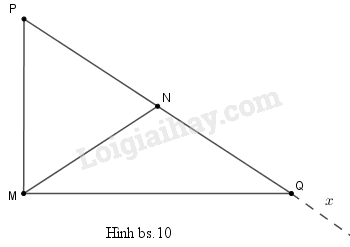
Tam giác MNP có \(MP = 6cm\), \(MN = PN = 5cm\). Góc \(MNx\) kề bù với góc góc \(MNP\). Điểm \(Q\) trên tia \(Nx\) sao cho \(NQ = NM\) (h.bs.10). Khi đó độ dài của đoạn thẳng \(PQ\) bằng

(A) \(5;  \)                                            (B) \(6;\)

(C) \(8;\)                                            (D) \(10.\)

Phương pháp giải:

Sử dụng công thức cộng độ dài: Nếu \(C\) nằm giữa \(A\) và \(B\) thì \(AC+CB=AB\)

Lời giải chi tiết:

Vì góc \(MNx\) kề bù với góc góc \(MNP\) nên hai tia \(NP\) và \(Nx\) đối nhau.

Mà điểm \(Q\) trên tia \(Nx\) nên \(N\) nằm giữa \(P\) và \(Q\)

Suy ra: \(PQ=PN+NQ\)\(=5+5=10\,cm\)

Đáp án đúng (D) \(10.\)

Loigiaihay.com