-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 164 trang 101 SBT Toán 8 tập 1
Giải bài 164 trang 101 sách bài tập toán 8. Cho đoạn thẳng AB = a. Gọi M là một điểm nằm giữa A và B. Vẽ về một phía của AB các hình vuông AMNP, BMLK có tâm theo thứ tự là C, D...
Đề bài
Cho đoạn thẳng AB = a. Gọi M là một điểm nằm giữa A và B. Vẽ về một phía của AB các hình vuông AMNP, BMLK có tâm theo thứ tự là C, D. Gọi I là trung điểm của CD.
a. Tính khoảng cách từ I đến AB
b. Khi điểm M di chuyển trên đoạn thẳng AB thì điểm I di chuyển trên đường nào ?
Phương pháp giải - Xem chi tiết
- Vận dụng tính chất của tam giác cân và tính chất về giao điểm hai đường chéo của hình vuông.
- Xác định khoảng cách giữa I với đoạn thẳng AB.
Lời giải chi tiết
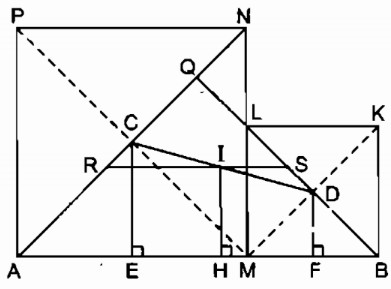
a. Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB
⇒ CE // DF // IH (cùng vuông với AB)
Suy ra DCEF là hình thang.
Xét hình thang DCEF có:
CE // DF // IH và IC = ID (vì I là trung điểm của CD)
Nên H là trung điểm cạnh EF
Suy ra IH là đường trung bình của hình thang DCEF
\( \Rightarrow IH = \displaystyle {{DF + CE} \over 2}\) (1)
Vì C là tâm hình vuông AMNP nên \(CA=CM\) (tính chất) và \(\widehat{ACM}=90^0\)
⇒ ∆ CAM là tam giác vuông cân tại C
Lại có CE ⊥ AM hay CE là đường cao của tam giác cân CAM
⇒ CE cũng là đường trung tuyến (tính chất tam giác cân)
⇒ CE = \(\displaystyle {1 \over 2}\)AM (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Vì D là tâm hình vuông BMLK nên \(DB=DM\) (tính chất) và \(\widehat{MDB}=90^0\)
⇒ ∆ DBM vuông cân tại D
Có DF ⊥ BM nên DF là đường cao của tam giác cân DBM
⇒ DF cũng là đường trung tuyến (tính chất tam giác cân)
⇒ DF = \(\displaystyle {1 \over 2}\)BM (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Vậy CE + DF = \(\displaystyle {1 \over 2}\)AM + \(\displaystyle {1 \over 2}\)BM
= \(\displaystyle {1 \over 2}\) (AM + BM) = \(\displaystyle {1 \over 2}\)AB = \(\displaystyle {a \over 2}\)
Từ (1) ta suy ra:
\( \Rightarrow IH = \displaystyle {{DF + CE} \over 2}\) \(=\displaystyle {{\displaystyle {a \over 2}} \over 2} = {a \over 4}\)
b. Gọi Q là giao điểm của BL và AN
Ta có: AN ⊥ MP (2) (tính chất hình vuông APNM)
BL ⊥ MK (3) (tính chất hình vuông BMLK)
Lại có: \(\widehat {PMN} = \dfrac{1}{2}\widehat {AMN} = \dfrac{1}{2}{.90^0} = {45^0}\) (do APNM là hình vuông nên MP là phân giác góc AMN)
\(\widehat {KMN} = \dfrac{1}{2}\widehat {BML} = \dfrac{1}{2}{.90^0} = {45^0}\) (do BMLK là hình vuông nên MK là phân giác góc BML)
\( \Rightarrow \widehat {PMK} = \widehat {PMN} + \widehat {NMK} \)\(= {45^0} + {45^0} = {90^0}\)
Suy ra MP ⊥ MK (4)
Từ (2), (3) và (4) suy ra BL ⊥ AN
Lại có \(\widehat {QAB} = \dfrac{1}{2}\widehat {MAP} \)\(= \dfrac{1}{2}{.90^0} = {45^0}\) (do APNM là hình vuông)
⇒ ∆ QAB vuông cân tại Q cố định.
Khi M thay đổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng \(\displaystyle {a \over 4}\) nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng \(\displaystyle {a \over 4}\)
Khi M trùng B thì I trùng với S là trung điểm của BQ
Khi M trùng với A thì I trùng với R là trung điểm của AQ
Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng \(\displaystyle {a \over 4}\) .
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.1 phần bài tập bổ sung trang 101 SBT Toán 8 tập 1
- Bài 1.2 phần bài tập bổ sung trang 101 SBT Toán 8 tập 1
- Bài 163 trang 100 SBT Toán 8 tập 1
- Bài 162 trang 100 SBT Toán 8 tập 1
- Bài 161 trang 100 SBT Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
