-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3, 4, 5. Những hằng đẳng thức đáng nhớ
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Bài tập ôn chương 1 - Phép nhân và phép chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Bài tập ôn chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - SBT TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM
-
Bài 163 trang 100 SBT Toán 8 tập 1
Giải bài 163 trang 100 sách bài tập toán 8. Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD. a. Tứ giác DEBF là hình gì ? Vì sao ? b. Chứng minh rằng các đường thẳng AC, BD, EF ...
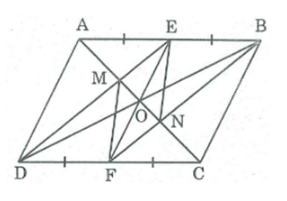
Đề bài
Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD.
a. Tứ giác DEBF là hình gì ? Vì sao ?
b. Chứng minh rằng các đường thẳng AC, BD, EF cùng cắt nhau tại một điểm.
c. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng tứ giác EMFN là hình bình hành.
Phương pháp giải - Xem chi tiết
- Dấu hiệu nhận biết hình bình hành: Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành
- Tính chất về các cạnh và đường chéo của hình bình hành.
Lời giải chi tiết
a) Xét tứ giác DEBF: AB // CD (vì ABCD là hình bình hành) hay DF // EB
EB = \(\displaystyle {1 \over 2}\)AB (do E là trung điểm của AB)
DF = \(\displaystyle {1 \over 2}\)CD (do F là trung điểm của DC)
Mà AB=CD (do ABCD là hình bình hành)
Suy ra: EB = DF
Vậy tứ giác DEBF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
b) Gọi O là giao điểm của AC và BD
OB = OD (tính chất hình bình hành ABCD)
Vì tứ giác DEBF là hình bình hành nên EF và BD cắt nhau tại trung điểm của mỗi đường
Suy ra: EF đi qua trung điểm O của BD
Vậy AC, BD và EF cắt nhau tại O trung điểm của mỗi đoạn
c. Vì DEBF là hình bình hành nên DE//BF
Suy ra \(\widehat {MEO} = \widehat {NFO}\) (so le trong)
Xét ∆ EOM và ∆ FON:
\(\widehat {MEO} = \widehat {NFO}\) (chứng minh trên)
OE = OF (tính chất hình bình hành DEBF)
\(\widehat {MOE} = \widehat {NOF}\) (đối đỉnh)
Do đó : \(∆ EOM = ∆ FON (g.c.g)\)\( ⇒ OM = ON\)
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 164 trang 101 SBT Toán 8 tập 1
- Bài 1.1 phần bài tập bổ sung trang 101 SBT Toán 8 tập 1
- Bài 1.2 phần bài tập bổ sung trang 101 SBT Toán 8 tập 1
- Bài 162 trang 100 SBT Toán 8 tập 1
- Bài 161 trang 100 SBT Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho Lớp 8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
